VGGT: Visual Geometry Grounded Transformer
摘要三维计算机视觉通常被约束在单个任务中,因此我们提出了VGGT,一个前馈神经网络,直接推理场景的所有三维属性,包括相机参数,点云,深度图和三维点轨迹。同时该方法简单且效率高,可以在一秒内重建图像。 简介传统的三维重建任务采用视觉几何方法,但是会增加求解的复杂性和计算成本。DUSt3R等方法虽然能直接使用一个神经网络实现三维任务,但只能接受两个图像的输入,需要后处理来重建更多的图像。 VGGT不需要特定的网络,使用的是标准的transformer结构,在大规模公开数据集上训练。尽管存在潜在的冗余,但学习预测这些相互关联的3D属性可以提高整体准确性。在推理过程中,我们可以从单独预测的深度和相机参数中推导出点云,相比使用点云head可以得到更高的精度。 方法 问题定义和符号输入是$N$张图像$I_i \in \mathbb{R}^{3 \times H \times W}$ 的序列$(I_i)^N_{i=1}$,VGGT transofrmer将序列映射为对应的三维注释: f \left( (I_i)_{i=1}^N \right) = (\mathbf{g}_i, D_i,...
Amodal Depth Anything: Amodal Depth Estimation in the Wild
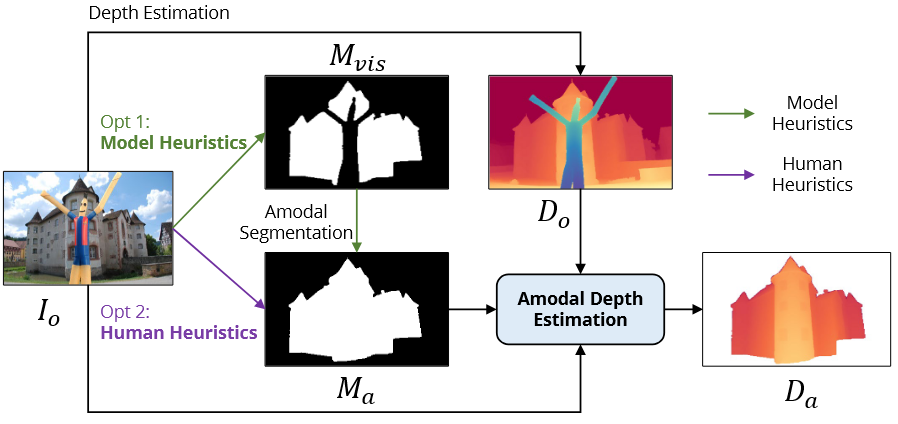
摘要Amodel 深度估计旨在预测场景中遮挡区域的物体的深度。这个任务可以解答模型是否可以根据可见的视觉线索感知到遮挡区域的几何关系。 提出了开放环境下amodel深度估计的全新范式,引入了一个新的大规模数据集Amodel Depth In the Wild(ADIW) 提出了两个互补的框架,一个基于Depth Anything V2的确定性模型AmodelDAV2,一个集成了条件流匹配原理的生成模型AmodelDepthFM 简介目前已有的方法在合成数据集上进行amodel的深度估计,但是合成数据获取成本高,与现实场景的复杂性与多样性存在差距。同时预测的绝对深度难以在数据有限的条件下泛化到未见过的场景上。 方法amodel深度估计旨在给定输入观察图像$I_o$、对应的深度图$D_o$和目标amodel分割mask $M_a$ 时,估计遮挡区域的深度值。 数据集构建 通过将对象放置在自然图像上来构建数据对。使用了图像分割数据集,相较于深度估计数据集规模更大。使用Segment...
Depth Prompting for Sensor-Agnostic Depth Estimation
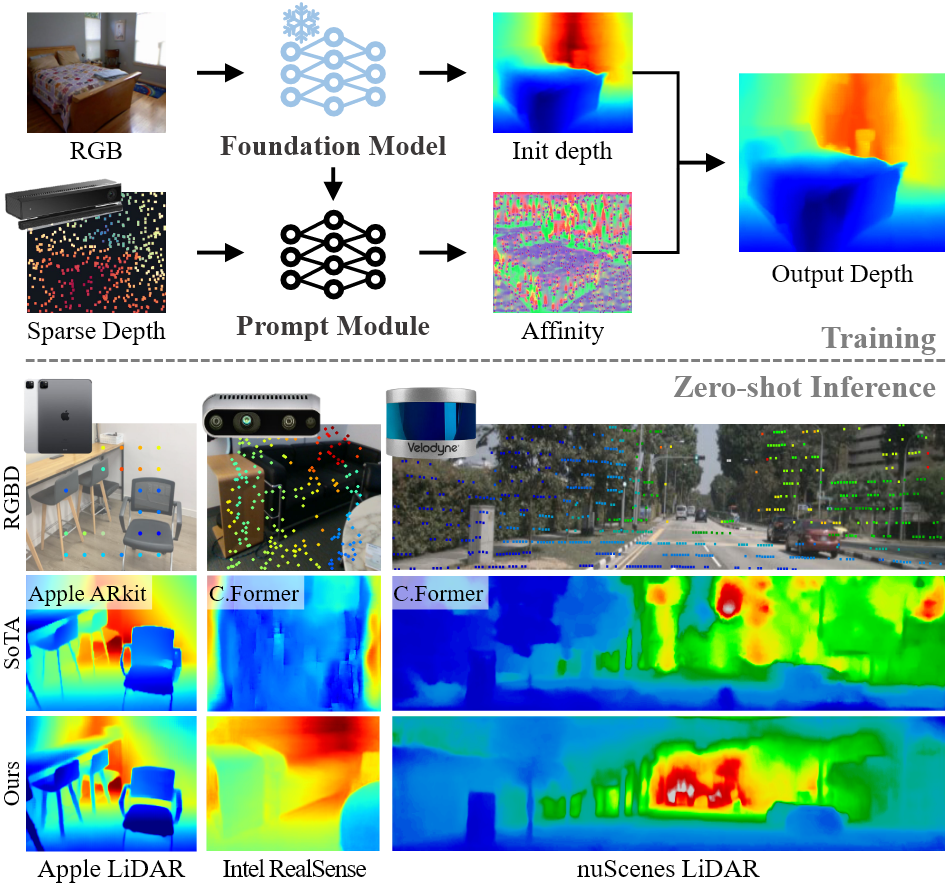
摘要由于系统性的测量偏差,例如密度、感知模式和扫描范围,当前方法在现实世界的应用范围有限。 学习联合表示的输入模式对偏差敏感。 设计了深度提示模块,根据传感器类型或场景配置的新深度分布获得希望的特征表示。 通过将这个模块嵌入基本的单目深度估计模型,可以解决深度扫描范围的限制,提供绝对的带尺度的深度图。 简介目标是构建一个传感器不可知的深度估计模型,能够在各种主动深度传感器上工作。深度提示首先编码稀疏的深度信息,并将其和图像特征进行融合构建一个逐像素的亲和力图。最后对亲和力图和最初的深度图进行细化操作。采用偏差调优技术,只需要对0.1%的模型参数进行微调。 Prompt EngineeringPrompt...
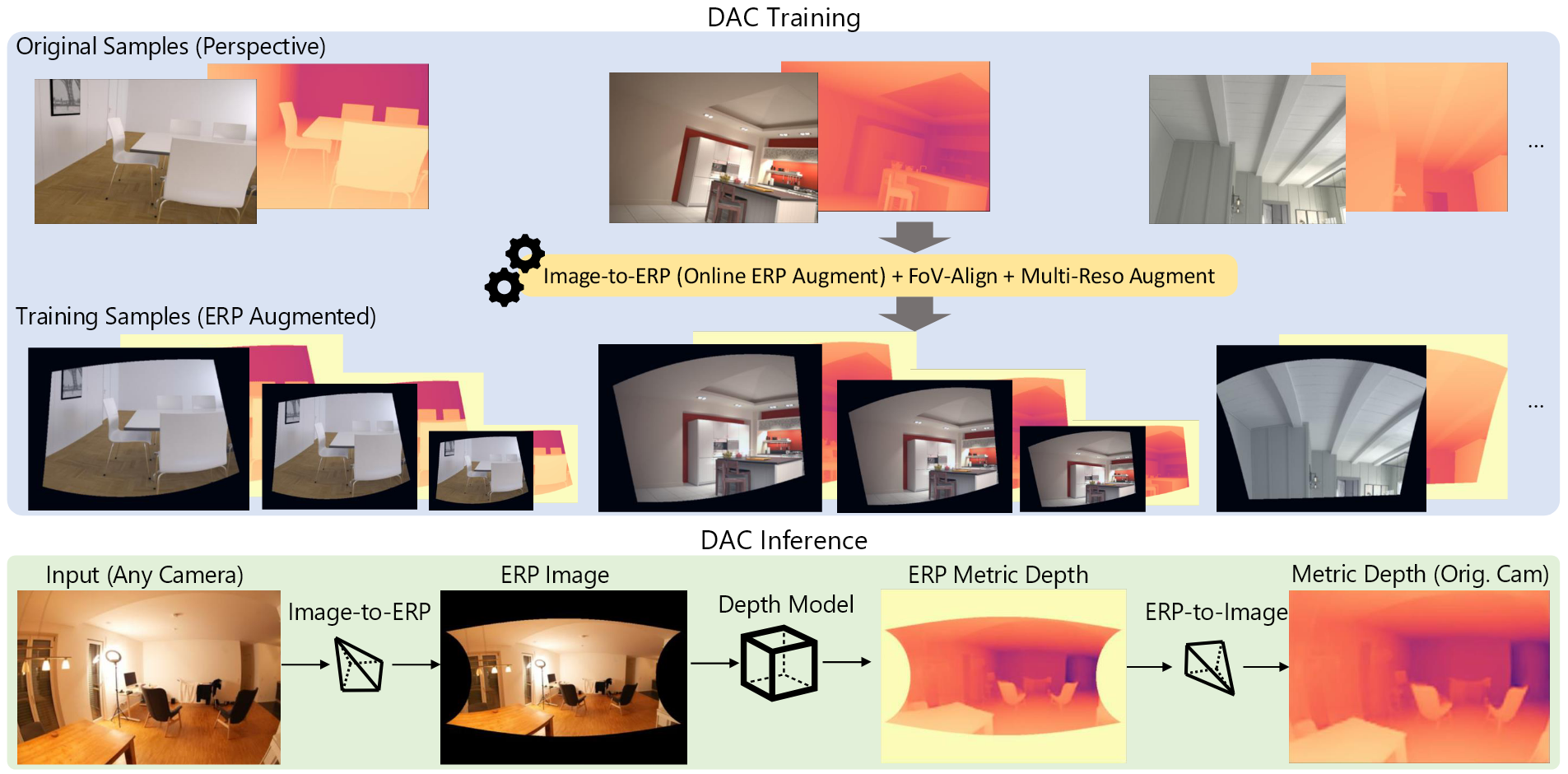
Depth Any Camera: Zero-Shot Metric Depth Estimation from Any Camera
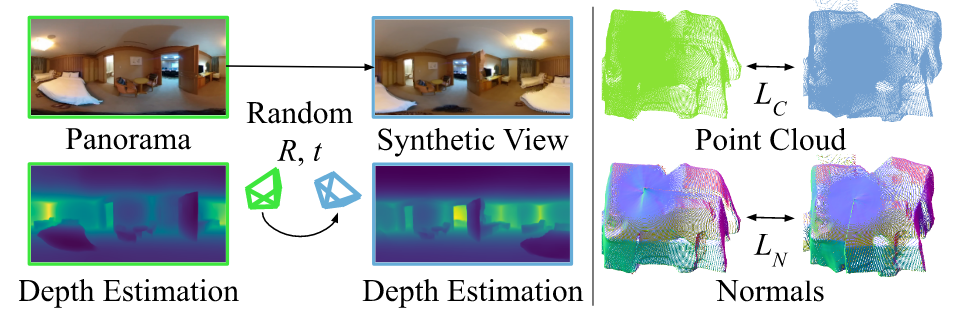
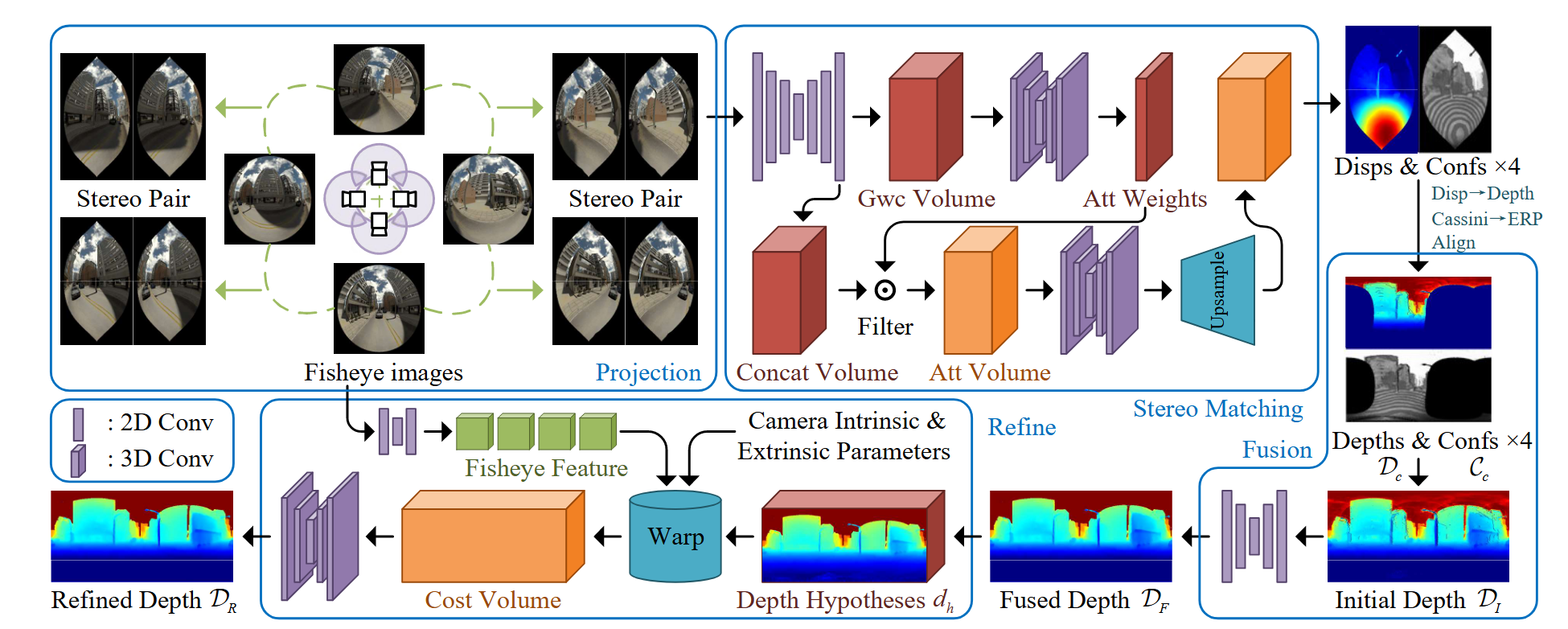
摘要虽然当前的深度基础模型展现出了强大的泛化能力,但对于不同的相机类型要获得精确的绝对深度仍然是一个具有挑战性的问题,尤其是对于大视场角的相机,例如鱼眼和360度相机。 提出了一个零样本的的绝对深度估计框架Depth Any...
Reconstruction vs. Generation: Taming Optimization Dilemma in Latent Diffusion Models
摘要具有Transformer架构的潜在扩散模型在生成高保真图像方面表现出色。然而近期的研究揭示了这种两阶段设计中的优化困境:虽然增加视觉 tokenizers 中每一个 token 的特征维度能够改善重建质量,但是需要更大的扩散模型和更多的训练迭代来实现可比的生成性能。 现有的系统得到的是次优的解决方案,由于 tokenizers 中信息的损失会产生视觉伪影,由于高昂的计算成本而无法完全收敛。 上述困境来源于学习无约束高维潜在空间的固有困难。 提出在训练视觉 tokenizers 的时候将潜在空间和预训练的视觉基础模型相对齐。提出VA-VAE(视觉基础模型对齐的变分自编码器),使DiT在高维潜在空间获得更快地收敛。 构建了增强的DiT基线,改善了训练策略和结构设计,称为LightingDiT。 贡献提出的视觉基础模型对齐损失解决了潜在扩散模型中的优化困境,使DiT在高维...
Improving the Diffusability of Autoencoders
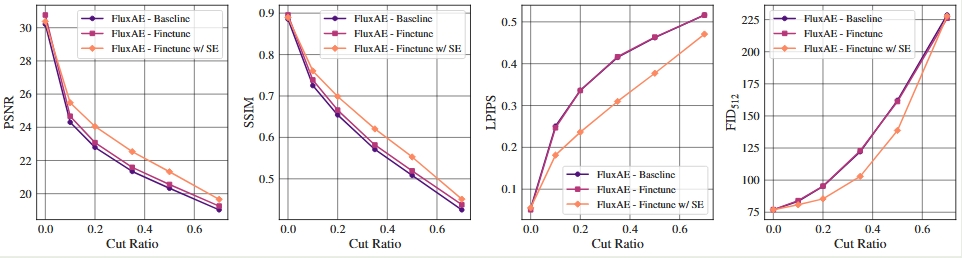
摘要鲜有人研究autoencoder和diffusion model之间的相互作用 autoencoder潜在空间中的高频分量会影响diffusion生成过程与质量 提出scale equivariance的正则化策略,在decoder中对潜在空间与RGB空间进行频率对齐 只需要改变较少的代码,20K步autoencoder的微调,就能够提高生成质量 简介Diffusability描述了通过扩散过程对分布进行建模的难易程度:高Diffusability表示分布易于拟合,而低Diffusability则使过程更加复杂 扩散模型鼓励误差累积推迟到频谱的高频部分,但是如果autoencoder的潜在低频部分与RGB空间中的对应部分的对应关系丢失了,就会影响重建的准确性。 现有的autoencoders中的潜在空间中存在突出的高频分量,与RGB信号中的频谱分布存在明显偏离,会影响重建的RGB结果,造成明显的视觉伪影。 标准的KL正则化不足以处理频谱缺陷,甚至可能放大问题。 方法背景:Blockwise 2D DCT给定以为二维信号块...