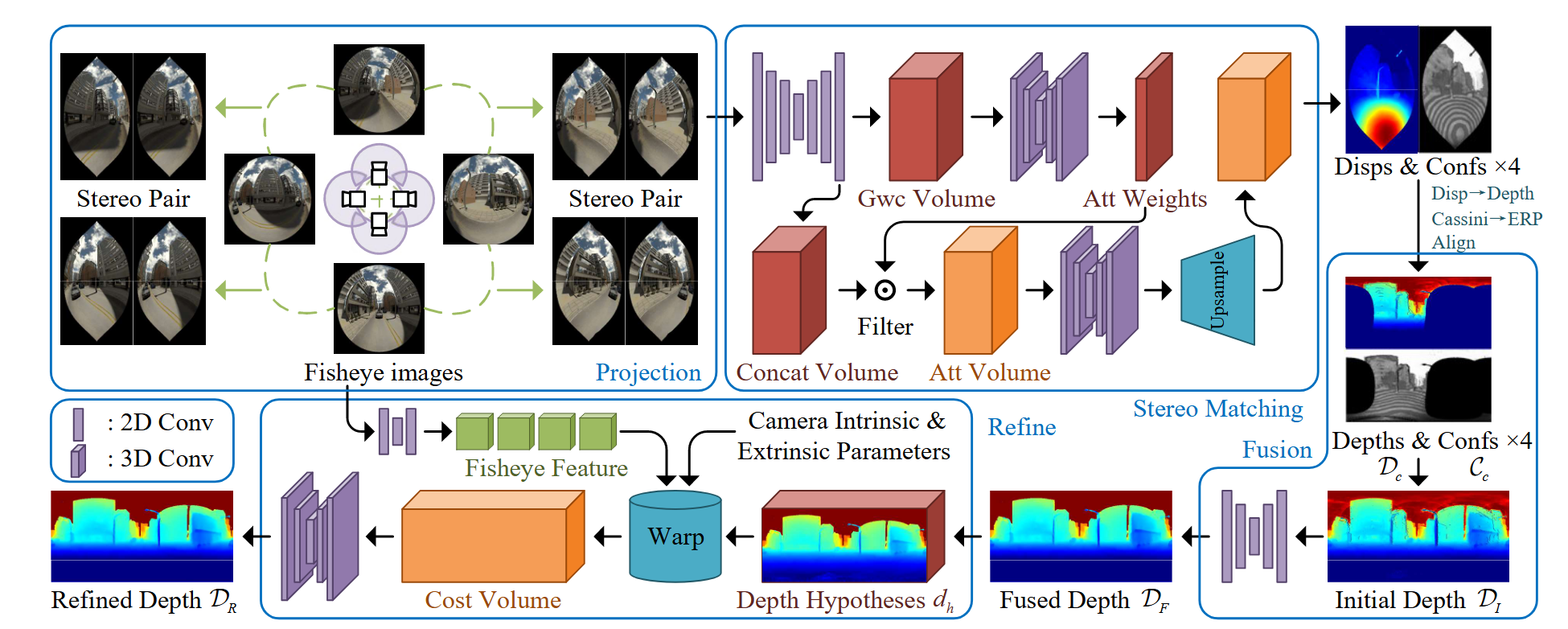
DIFFERENTIABLE 3D GAUSSIAN SPLATTING

3DGS1

3D高斯的优势：非结构化、可微、利用快速α混合进行渲染、无需法线

世界坐标系下，高斯由三维协方差矩阵和点（均值）μ表示：

$G ( x ) \,=e^{-\frac{1} {2} ( x )^{T} \Sigma^{-1} ( x )} \tag{4}$

给定视角变换矩阵W，相机坐标系下的协方差矩阵为：

$\Sigma^{\prime}=J W \Sigma W^{T} J^{T} \tag{5}$

其中J是投影变换的仿射近似雅可比矩阵

协方差矩阵只有在半正定的时候才具有物理意义，而如果直接对协方差矩阵使用梯度下降优化，很难保证矩阵的合理性。

由于协方差矩阵是用来描述椭球的形状，因此可以用缩放矩阵S和旋转矩阵R来获得一个对应的协方差矩阵：

$\Sigma=R S S^{T} R^{T}\tag{6}$

OPTIMIZATION WITH ADAPTIVE DENSITY CONTROL OF 3D GAUSSIANS

Optimization

优化的参数：位置p，α，协方差矩阵，球谐函数系数

$\mathcal{L}=( 1-\lambda) \mathcal{L}_{1}+\lambda\mathcal{L}_{\mathrm{D-S S I M}} \tag{7}$

Adaptive Control of Gaussians

we densify every 100 iterations and remove any Gaussians that are essentially transparent, i.e., with 𝛼 less than a threshold 𝜖𝛼 .

we densify Gaussians with an average magnitude of view-space position gradients above a threshold 𝜏pos, which we set to 0.0002 in our tests.

3DGS2

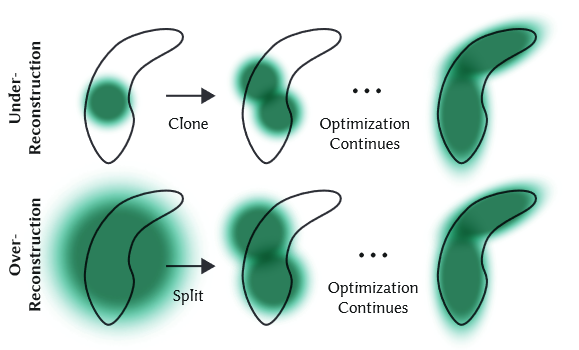
Similar to other volumetric representations, our optimization can get stuck with floaters close to the input cameras; in our case this may result in an unjustified increase in the Gaussian density.

An effective way to moderate the increase in the number of Gaussians is to set the 𝛼 value close to zero every 𝑁 = 3000 iterations.

FAST DIFFERENTIABLE RASTERIZER FOR GAUSSIANS

splitting the screen into 16×16 tiles

cull 3D Gaussians against the view frustum and each tile

We then instantiate each Gaussian according to the number of tiles they overlap and assign each instance a key that combines view space depth and tile ID.

sort Gaussians based on these keys using a single fast GPU Radix sort

After sorting Gaussians, we produce a list for each tile by identifying the first and last depth-sorted entry that splats to a given tile.