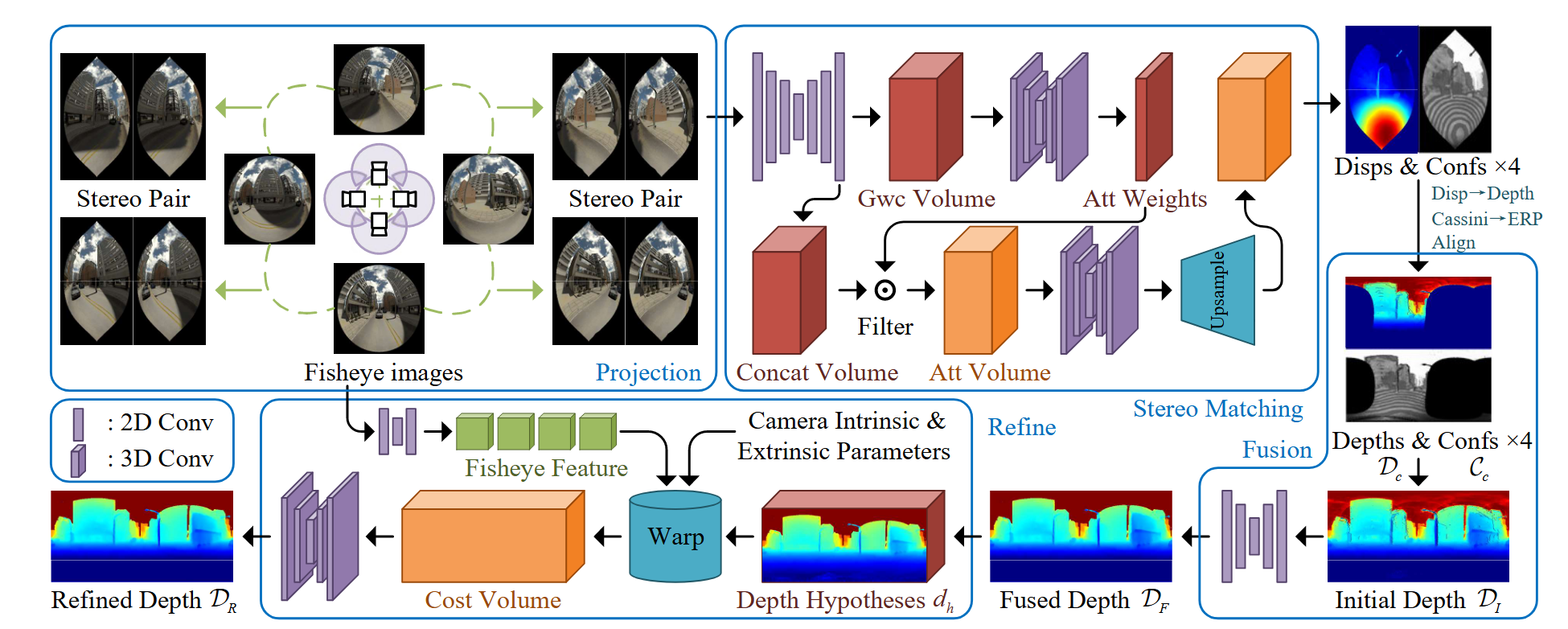
pixelSplat: 3D Gaussian Splats from Image Pairs for Scalable Generalizable 3D ReconstructionpixelSplat

3D GS中的局部最小值问题

在随机位置初始化的高斯，在移向最终位置的时候会出现局部最小值：

1.如果距正确位置的距离超出一定的标准差范围后，高斯元的梯度会消失

2.即使高斯足够接近一个“正确”的位置，仍然需要一个通向最终位置的路径，使得损失在路径上单调减少。

3D高斯虽然通过自适应的密度控制来让高斯移到最终的位置，但是这种方法与一般的设定不相容，一般来说参数都需要通过一个神经网络来预测，必须接收梯度。

以图像为条件的3DGS推理

解决尺度模糊问题

在理想情况下，新视角合成的数据集包含的相机位姿应当是metric的，每一个场景应当包含一系列元组

${\mathcal{C}}_{i}^{\mathrm{m}} =\{( \mathbf{I}_{j}, \mathbf{T}_{j}^{\mathrm{m}} ) \}_{j}$

包括图像和对应的真实世界尺度的位姿。

在实际的情况下，数据集中的位姿通常是使用SfM计算的，每一个场景都对应着不同的尺度，这时

$s_{i} \mathbf{T}_{j}^{\mathrm{m}}$

对应的才是metric的位姿。

pixelSplat1

给定两个参考视角 $\mathbf{I}$ 和 $\tilde{\mathbf{I}}$ ，对于 $\mathbf{I}$ 中的每一个像素点，可以用 $\mathbf{I}$ 中对应的深度值沿着 $\tilde{\mathbf{I}}$ 中的极线对该点进行注释。由于深度值是从 $\mathbf{I}$ 和 $\tilde{\mathbf{I}}$ 的相机位姿计算得到的，所以其自然包含了对场景尺度的编码。因此关键的思想就是找到每个像素的对应点及对应的深度值。

首先将两张图像都进行编码，得到对应的特征 $\mathbf{F}$ 和 $\tilde{\mathbf{F}}$ ，设 $\mathbf{u}$ 是 $\mathbf{I}$ 的像素坐标，$\ell$ 是将 $\mathbf{u}$ 的相机光线投影到 $\tilde{\mathbf{I}}$ 的图像平面上得到的极线。沿着 $\ell$ 采样像素坐标，对于每一个极线的样本都能够使用三角测量法，计算其到相机原点的距离。极线注意力的queries，keys和values用以下方式进行计算：

$\mathbf{s}=\tilde{\mathbf{F}} [ \tilde{\mathbf{u}}_{l} ] \oplus\gamma( \tilde{d}_{\tilde{\mathbf{u}}_{l}} ) \tag{1}$ ${\bf q}={\bf Q} \cdot{\bf F} [ {\bf u} ], \quad{\bf k}_{l}={\bf K} \cdot{\bf s}, \quad{\bf v}_{l}={\bf V} \cdot{\bf s}, \tag{2}$

$\oplus$ 表示连接操作，$\gamma()$ 表示位置编码，用极线注意力更新对应的特征：

$\mathbf{F} [ \mathbf{u} ]+=\mathbf{A t t} ( \mathbf{q}, \{\mathbf{k}_{l} \}, \{\mathbf{v}_{l} \} ), \tag{3}$

Att表示 softmax ，+=表示跳连接操作。每一个像素特征都包含了深度位置编码的加权和，正确的对应关系应当在权重最大处获得。因此，所编码的带尺度的深度就与随机尺度相一致了。在极线cross-attention后是每张图像的self-attention：

$\mathbf{F} +=\mathbf{SelfAttention}(\mathbf{F}) \tag{4}$

整个方法同样可以对多张图像输入使用。

高斯参数估计

对于坐标为 $\mathbf{u}$ 的每一个像素，用其对应的特征 $\mathbf{F} [ \mathbf{u} ]$ 作为输入预测高斯元的参数。

pixelSplat2

基线：预测 $\mu$ 的点估计

直接考虑对高斯的中心 $\mu$ 进行回归预测，即使用一个神经网络对高斯均值到相机原点的距离进行回归，然后将其投影到3D空间当中。

$\boldsymbol{\mu}=\mathbf{o}+d_{\mathbf{u}} \, \mathbf{d}, \, \, \, d=g ( \mathbf{F} [ \mathbf{u} ] ), \, \, \, \mathbf{d}=\mathbf{T} \mathbf{K}^{-1} [ \mathbf{u}, 1 ]^{T}\tag{5}$

但是直接回归很容易陷入局部最优。

预测 $\mu$ 的概率密度

预测高斯在沿着光线 $\mathbf{u}$ 深度为 $d$ 处存在的似然概率分布。设置近平面和远平面 $d{near}$ $d{far}$ ，在这个区间内将深度值离散化为 $Z$ 个bins，在视差空间中所表示的第 $z$ 个元素为：

${\bf b}_{z}=\left( \left( 1-\frac{z} {Z} \right) \left( \frac{1} {d_{\mathrm{n c a r}}}-\frac{1} {d_{\mathrm{f a r}}} \right)+\frac{1} {d_{\mathrm{f a r}}} \right)^{-1}.\tag{6}$

定义的概率分布 $p_{\phi}(z)$ 参数为离散概率 $\phi$ ，其第 $z$ 个参数表示一个表面存在于深度 bucket $b_z$ 的概率。概率 $\phi$ 是通过一个全连接神经网络进行预测的，通过一个softmax归一化为和为一。然后预测了一个中心偏移值来调整bucket 边界之间高斯的深度。

$\mu=\mathbf{o}+\left( \mathbf{b}_{z}+\delta_{z} \right) \mathbf{d}_{\mathbf{u}}, \ z \sim p_{\boldsymbol{\phi}} ( z ), \ ( \boldsymbol{\phi}, \boldsymbol{\delta} )=f ( \mathbf{F} [ \mathbf{u} ] ) \tag{7}$