摘要

三维计算机视觉通常被约束在单个任务中，因此我们提出了VGGT，一个前馈神经网络，直接推理场景的所有三维属性，包括相机参数，点云，深度图和三维点轨迹。同时该方法简单且效率高，可以在一秒内重建图像。

简介

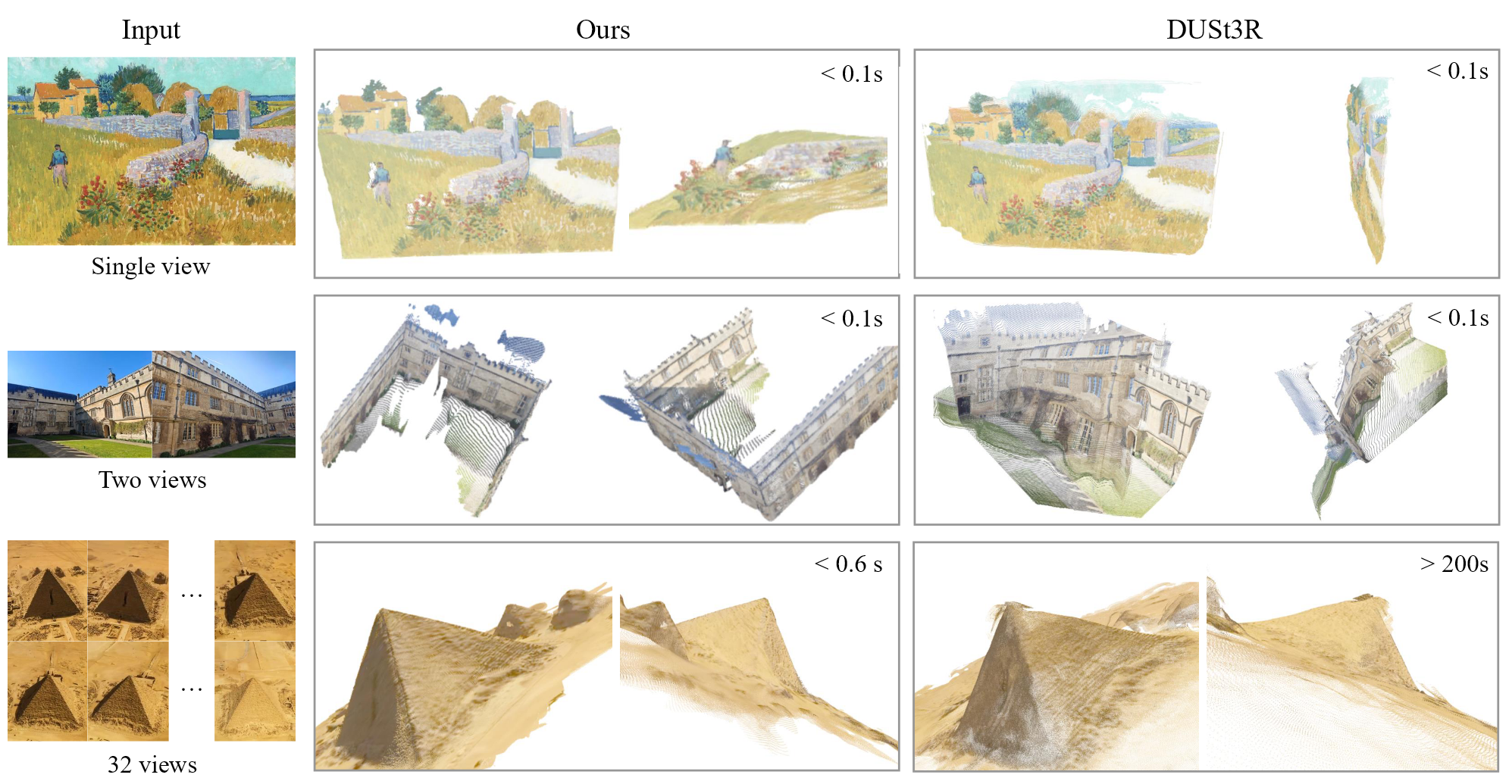
传统的三维重建任务采用视觉几何方法，但是会增加求解的复杂性和计算成本。DUSt3R等方法虽然能直接使用一个神经网络实现三维任务，但只能接受两个图像的输入，需要后处理来重建更多的图像。

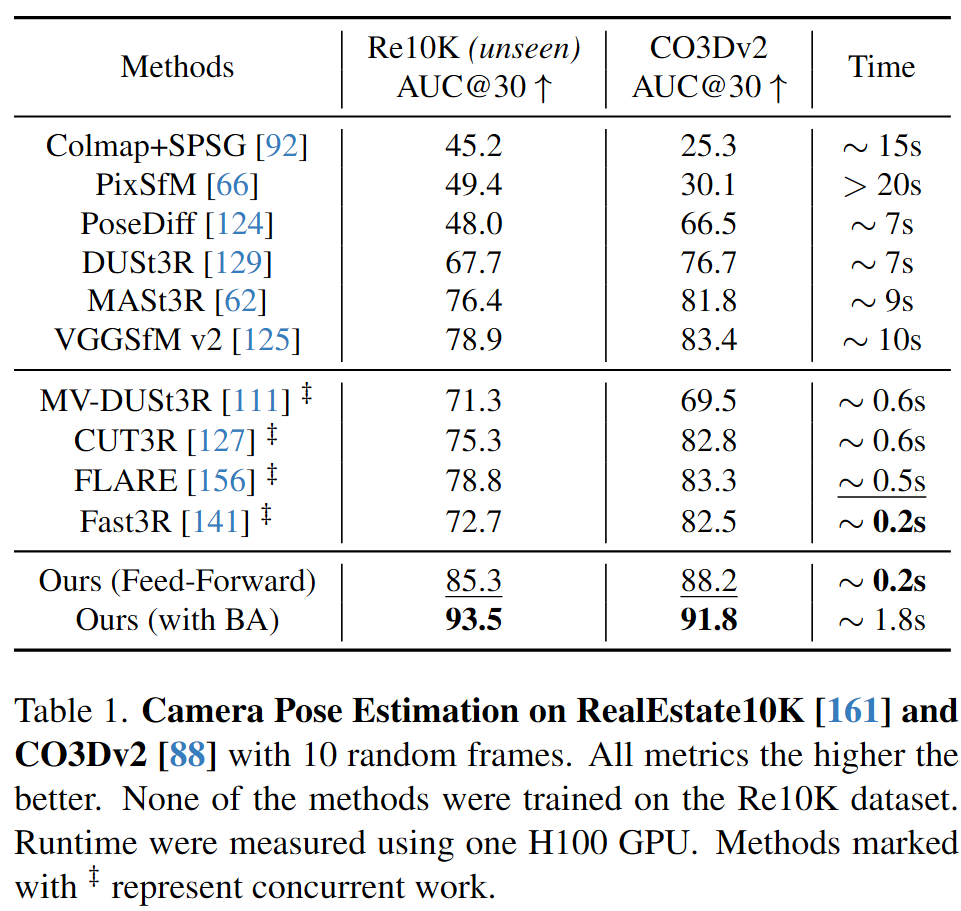
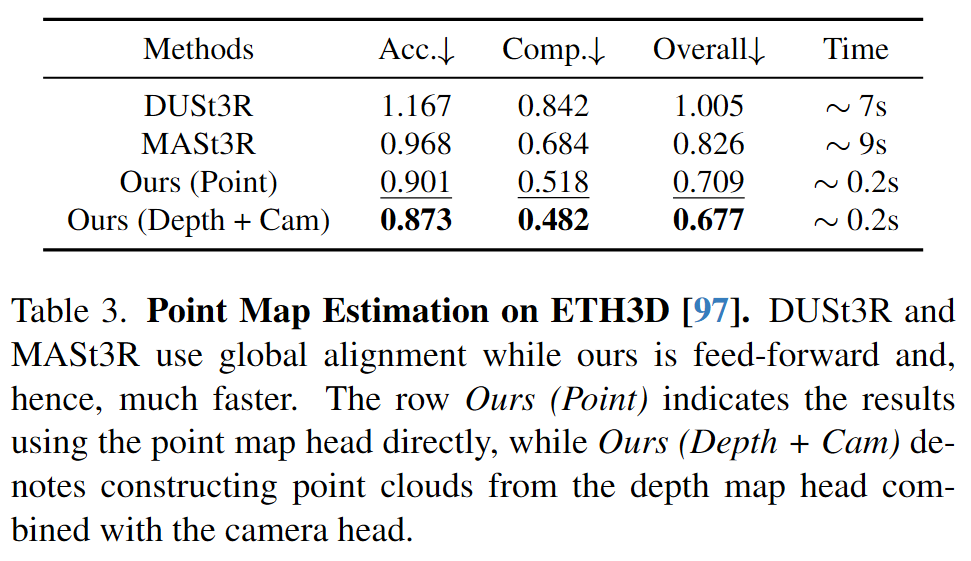
VGGT不需要特定的网络，使用的是标准的transformer结构，在大规模公开数据集上训练。尽管存在潜在的冗余，但学习预测这些相互关联的3D属性可以提高整体准确性。在推理过程中，我们可以从单独预测的深度和相机参数中推导出点云，相比使用点云head可以得到更高的精度。

方法

VGGT-1

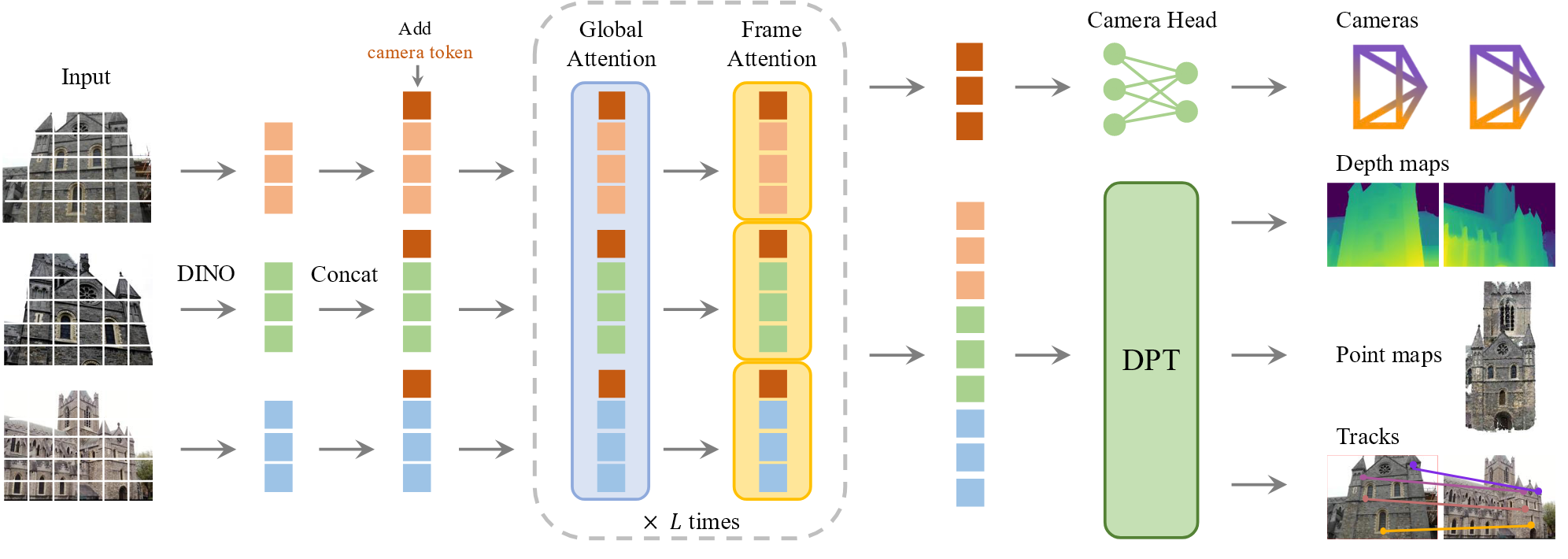
问题定义和符号

输入是$N$张图像$I_i \in \mathbb{R}^{3 \times H \times W}$ 的序列$(I_i)^N_{i=1}$，VGGT transofrmer将序列映射为对应的三维注释：

$f \left( (I_i)_{i=1}^N \right) = (\mathbf{g}_i, D_i, P_i, T_i)_{i=1}^N$

$\mathbf{g}_i \in \mathbb{R}^9$ 是内参和外参，$D_i \in \mathbb{R}^{H \times W}$是深度图，$P_i \in \mathbb{R}^{3\times H \times W}$是点云图，用于点跟踪的$C$维特征网络$T_i \in \mathbb{R}^{C \times H \times W}$。

$\mathbf{g}_i$ 是旋转四元数$\mathbf{q}\in \mathbb{R}^4$，平移向量$\mathbf{t}\in \mathbb{R}^3$和视场角$\mathbf{f}\in \mathbb{R}^2$ 的组合，$\mathbf{g}=[\mathbf{q},\mathbf{t},\mathbf{f}]$。假设相机的原点在图像中心。

用$\mathcal{I}(I_i) = {1, \dots, H} \times {1, \dots, W}$表示图像像素位置的集合。深度图$D_i$将每个像素位置$\mathbf{y}\in \mathcal{I}(I_i)$与对应的深度值 $D_i(\mathbf{y}) \in \mathbb{R}^{+}$联系起来。相同的点云图$P_i$将每个像素和对应的三维场景点$P_i(\mathbf{y})\in \mathbb{R}^3$ 。与DUSt3R相同，三维点$P_i(\mathbf{y})$是在第一个相机$\mathbf{g}_1$的坐标系统上定义的。

对于点追踪，给定查询图像$I_q$中固定的查询点$\mathbf{y}_q$，网络输出所有图像$I_i$中对应二维点$\mathbf{y}_i\in\mathbb{R}^2$ 的追踪，$\mathcal{T}*(\mathbf{y}_q)=(\mathbf{y_i}^N_{i=1})$。tracking是由一个单独的模块计算的，公式为：

$\mathcal{T}((\mathbf{y}_j)_{j=1}^M, (T_i)_{i=1}^N) =((\hat{\mathbf{y}}_{j,i})_{i=1}^N)_{j=1}^M$

参考帧是选定的第一张图像，其他图像是随机的。

网络预测的属性并不都是独立的，例如相机参数可以通过对点云图求解PnP问题得到，深度图也可以通过点云图和相机参数推导。但是让VGGT对这些属性显式地预测可以得到显著的提升。在推理过程中，利用预测的相机参数和深度图可以产生更加精确的三维点。

特征骨干网络

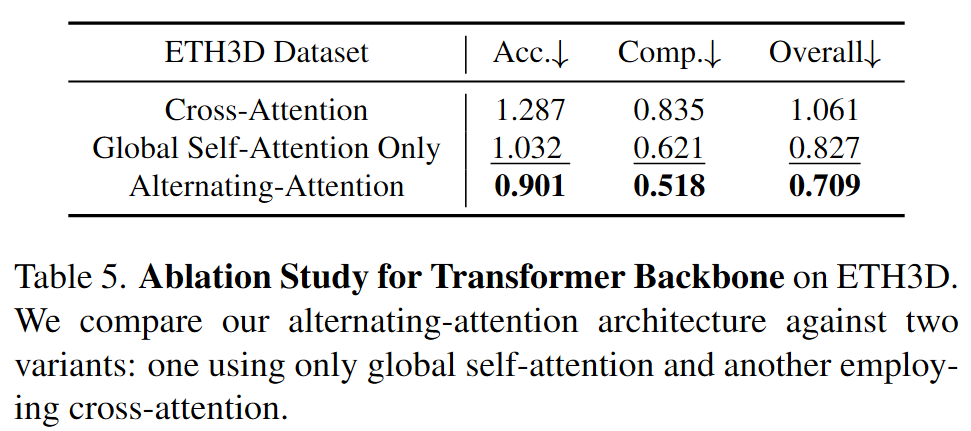
使用的模型是一个大型的transformer，每一张输入图像初始通过DINO被分块成$K$个tokens的集合$t^I\in\mathbb{R}^{K\times C}$。所有帧的图像tokens组合$t^{\mathbf{I}} = \cup^{N}_{i=1}x { t_{i}^{\mathbf{I}} }$随后通过主网络结构，交替逐帧和全局self-attention层。

我们引入了交替注意力（AA）机制，以交替的形式聚焦每一帧和全局。具体而言，分别对每一帧的tokens $\mathbf{t}^I_k$应用逐帧的self-attention。并对所有帧的tokens $\mathbf{t}^I$使用全局的self-attention。默认使用了二十四层全局和逐帧的注意力层。

预测头

对于每一个输入图像的token，添加额外的相机token $\mathbf{t}^g_i\in \mathbb{R}^{1 \times C’}$ 和四个register tokens $\mathbf{t}^R_i \in \mathbb{R}^{4 \times C’}$ ，将连接的 $(t^{I}_{i}, t^{I}_{g}, t^{j}_{R})_{j=1}^{N}$ 传入AA transformer得到输出的tokens $(\hat{t}^{I}_{i}, \hat{t}^{I}_{g}, \hat{t}^{j}_{R})_{j=1}^{N}$ ，第一帧 $(t^{g}_{1} := \overline{t}^{g}, t^{R}_{1} := \overline{t}^{R})$ 的相机token 和register token $\overline{t}^g,\overline{t}^R$ 被设置为其他帧 $(t^g_i := \overline{\overline{t}}^{g}, t^{R}_{i}:= \overline{\overline{t}}^{R}, i \in [2, \dots, N])$ 不同的可学习的tokens 。这样可以让模型分辨出第一帧，从而在第一个相机的坐标系下表示三维预测。

坐标系帧第一个相机的相机外参被设置为单位阵，及旋转四元数为$\mathbf{q}_1=[0,0,0,1]$，平移向量为$\mathbf{t}_1=[0,0,0]$。

相机预测相机参数$(\hat{\mathbf{g}}^i)^N_{i=1}$用四个额外的self-attention层和线性层从相机tokes $(\hat{\mathbf{t}}^i)^N_{i=1}$ 中预测得到。

稠密预测输出的图像tokens $\hat{\mathbf{t}}^I_i$用来预测稠密的输出。 $\hat{\mathbf{t}}^I_i$首先用DPT层转换为稠密的特征图$F_i \in \mathbb{R}^{C’’ \times H \times W}$，每一个$F_i$用一个3×3的卷积层映射为对应的深度和点图。此外，DPT头还输出稠密的特征$T_i$用于tracking头的输入。同时，我们还预测了每一个深度图和点图的任意不确定性 $\Sigma^{D}_{i} \in \mathbb{R}_{+}^{H \times W}$ 和 $\Sigma^{P}_{i} \in \mathbb{R}_{+}^{H \times W}$ ，用于计算损失，与模型的置信度成正比。

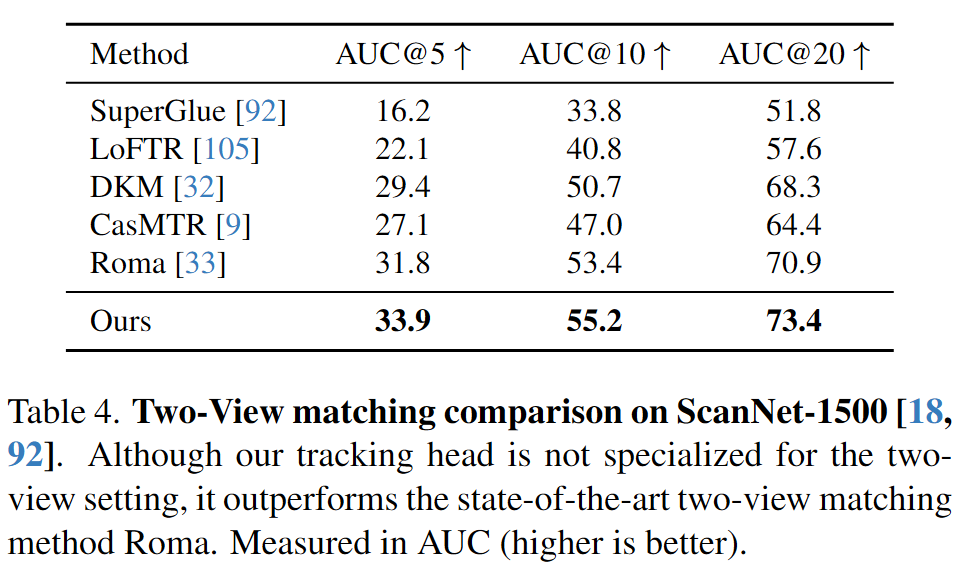
Tracking 使用CoTracker2结构，输入为稠密的tracking特征$T_i$ ，给定查询图像$I_q$中的一个查询点$\mathbf{y}_j$，$\mathcal{T}$预测所有图像中对应于相同三维点的二维点集$\mathcal{T}((\mathbf{y}_j)^M_{j=1}, (T_i)^N_{i=1}) =((\hat{\mathbf{y}}_{j,i})^N_{i=1})^M_{j=1}$。查询图像的特征图首先在查询点进行双线性采样得到特征，然后和其他特征图的特征联系在一起获得相关性图集合。然后通过self-attention层来预测最终的二维点。

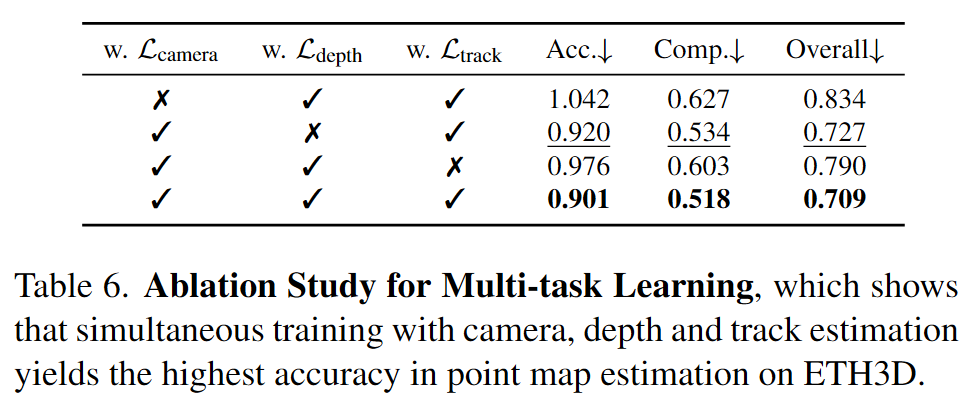
训练

采用多任务损失：

$\mathcal{L} = \mathcal{L}_{\text{camera}} + \mathcal{L}_{\text{depth}} + \mathcal{L}_{\text{pmap}} + \lambda \mathcal{L}_{\text{track}}. \tag{2}$

$\lambda=0.05$

$\mathcal{L}_{\text{camera}} = \sum_{i=1}^{N} \|\mathbf{g}_i - \mathbf{\hat{g}}_i\|_c$ $\mathcal{L}_{\text{depth}} = \sum_{i=1}^{N} \| \Sigma_{i}^{D} \odot (\hat{D}_{i} - D_{i}) \| + \| \Sigma_{i}^{D} \odot (\nabla \hat{D}_{i} - \nabla D_{i}) \| - \alpha \log \Sigma_{i}^{D}$

$\odot$表示通道传播逐元素乘积

$\mathcal{L}_{\text{pmap}} = \sum_{i=1}^{N} \| \Sigma_{i}^{P} \odot (\hat{P}_{i} - P_{i}) \| + \| \Sigma_{i}^{P} \odot (\nabla \hat{P}_{i} - \nabla P_{i}) \| - \alpha \log \Sigma_{i}^{P}$ $\mathcal{L}_{\text{track}} = \sum_{j=1}^{M}\sum_{i=1}^{N} \| \mathbf{y}_{j,i} - \hat{\mathbf{y}}_{j,i} \|$

Ground Truth 坐标归一化 首先表示第一个相机坐标系下所有的量，然后计算点云中所有三维点到原点的平均欧拉距离，并用这个尺度归一化相机平移，点云和深度图。但是没有对预测的输出进行归一化，而是让transformer学习归一化。

参数规模 12亿 64 A100 GPUs over nine days.

数据集 Co3Dv2 , BlendMVS, DL3DV, MegaDepth, Kubric, WildRGB, ScanNet, HyperSim, Mapillary, Habitat , Replica, MVS-Synth, PointOdyssey, Virtual KITTI, Aria Synthetic Environments, Aria Digital Twin, and a synthetic dataset of artist-created assets similar to Objaverse