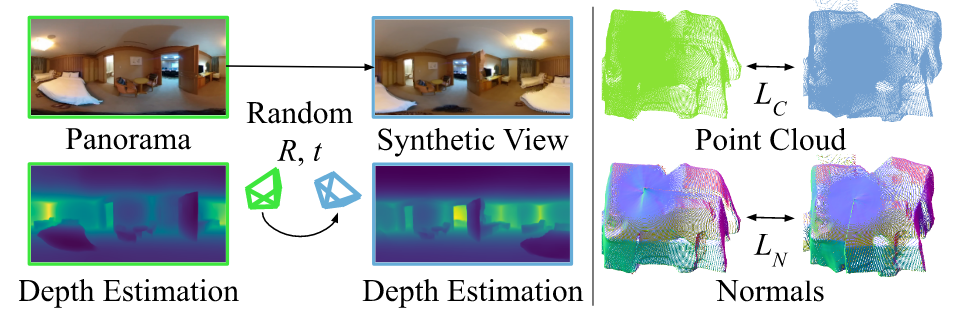
Evaluating Robustness of Monocular Depth Estimation with Procedural Scene Perturbations
摘要
在标准benchmark上测评的性能并不能完整地评估单目深度估计任务方法地鲁棒性。在本工作中,引入了程序化深度评估,能够系统性地进行鲁棒性评估。主要使用程序化生成来创建三维场景,评估对可控扰动的鲁棒性,包括物体、相机、材料和光照变化。
简介
标准的benchmarks不能够提供完整的性能的评估,大部分只评估精度,而不是鲁棒性,不能够说明在场景中存在扰动的情况下预测是否可行。不够鲁棒的模型容易出现不可预测的性能下降,容易受到对抗性攻击,并且无法部署在关键任务应用程序中。

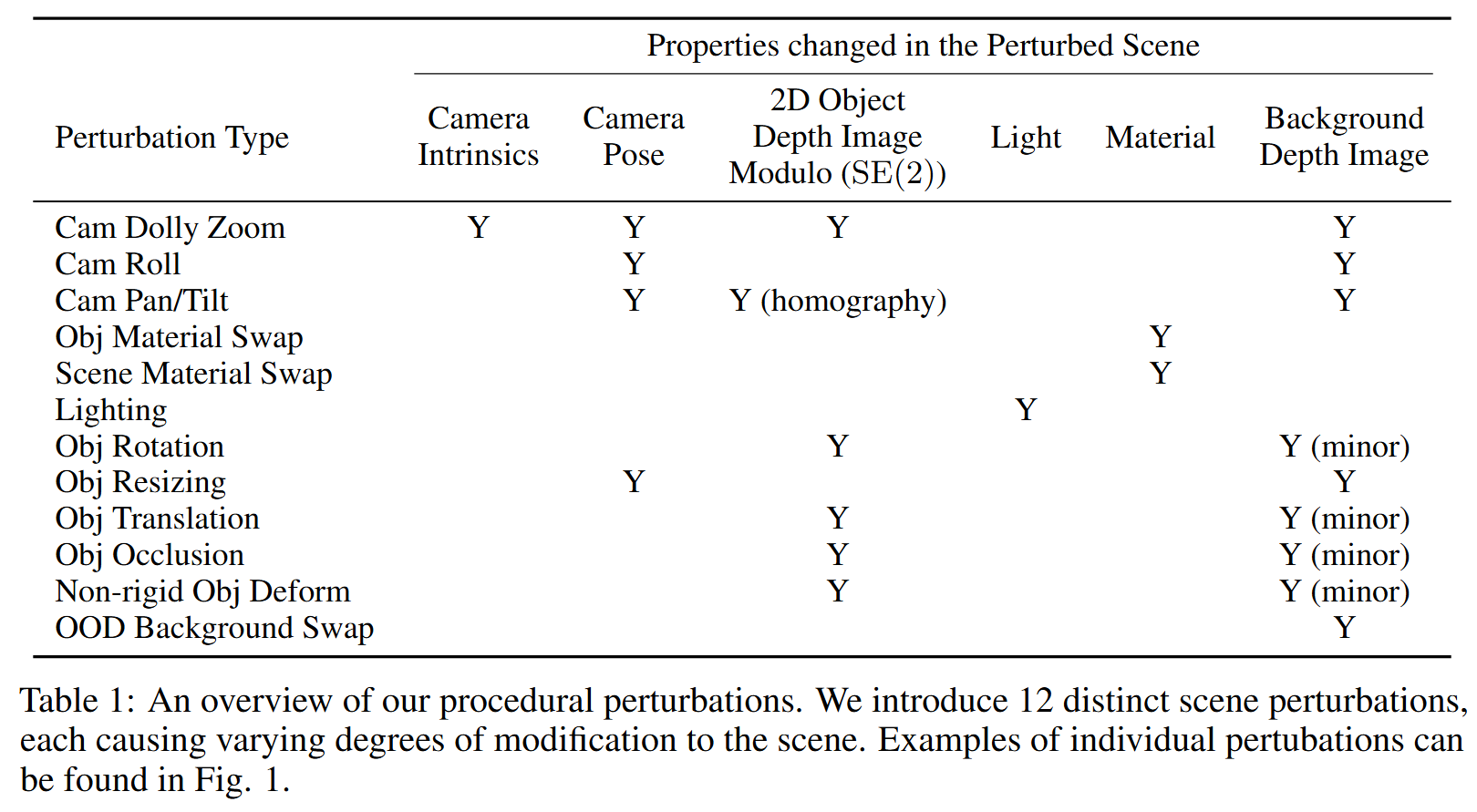
扰动的类型包括移动相机,改变相机内参,改变光照,该表材料,变形形状。使用Infinigen生成地室内和室外场景进行评估。Infinigen的程序性实际上保证了测试场景是新颖的,因此适合评估泛化和鲁棒性。Infiniten对象是完全程序化的,能够实现形状的非刚性和语义上有意义的变形。
引入两个鲁棒性的概念:精度稳定性和自洽性。精度稳定性是模型在扰动下的预测与地面真实值之间差异的方差。自洽性是通过模型在扰动下的预测与原始预测之间的平均(平方)差来衡量。
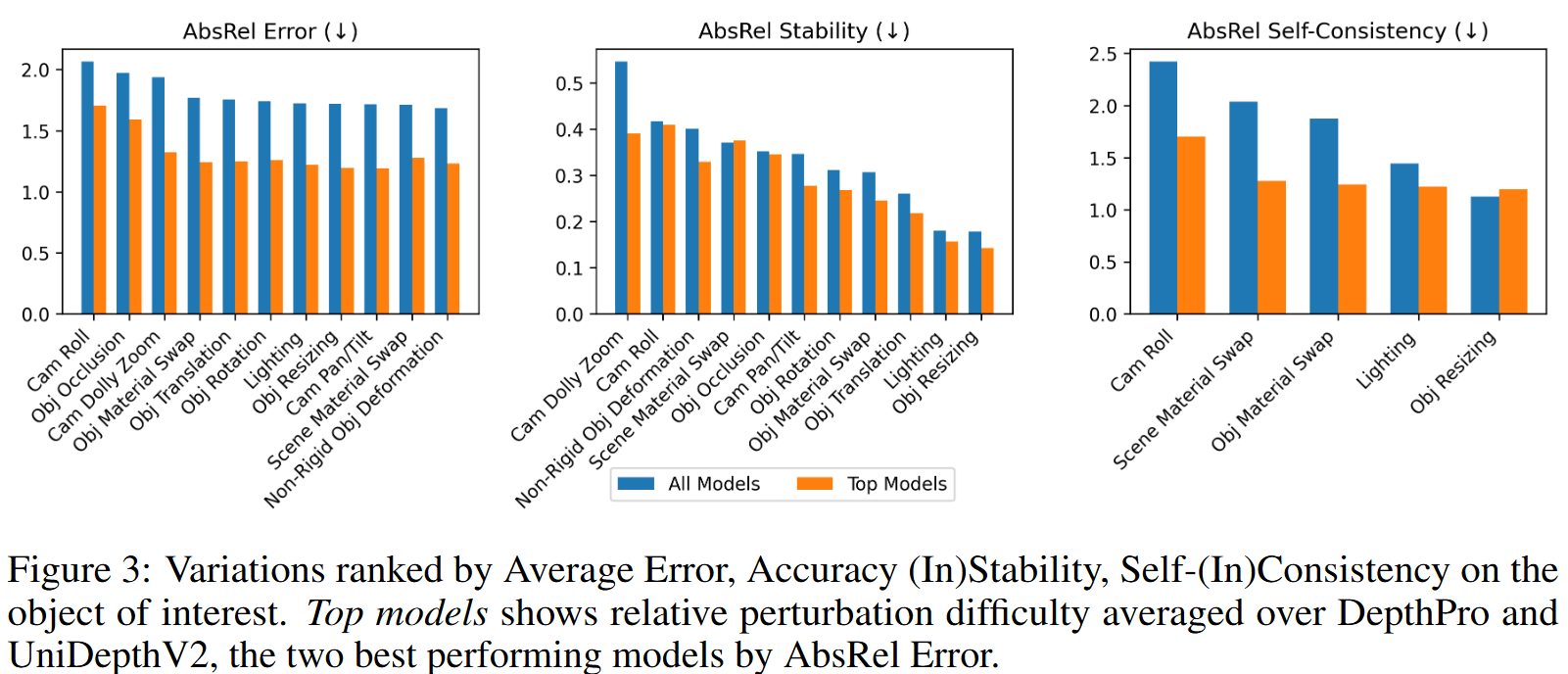
先进的深度估计模型相对于光照和三维物体姿态的扰动较为鲁棒,对遮挡和材质变化的鲁棒性较差。且相机扰动也十分具有挑战性。
方法
使用Infinigen Nature和Infinigen Indoors生成的场景来构建程序性深度评估。每一个场景都是用程序性生成从头开始生成。生成包含以下类别之一的感兴趣对象的场景:椅子、桌子、橱柜、鱼和仙人掌。选择这些类别来涵盖各种各样的自然和人造物体,每种物体都有不同的几何特征。PDE数据集包括5个对象类别和38个不同的场景,每个对象类别出现在8个场景中。共有12种可能的程序扰动,每种扰动最多有60种不同的参数设置。这导致总共13693个独特的场景变化,为模型鲁棒性提供了多样化和全面的评估。
程序性扰动
- 相机推拉变焦:改变相机的焦距,并前后移动相机使物体大小几乎保持不变
- 相机滚动:将相机绕其光轴旋转,保证相机中心固定。
- 相机平移/倾斜:将相机绕着Y轴或X轴进行旋转,保证相机中心固定。
- 物体材料转换:随机改变某一感兴趣的物体的材料
- 场景材料转换:随机改变场景中所有物体的材料
- 光照:添加或移除光源,改变强度和温度,或者改变光的类型
- 物体旋转:将物体绕着其局部参照系的原点旋转
- 物体平移:移动物体且不改变物体的旋转
- 物体缩放:缩放物体,使其相对于场景的其他部分更大。同时移动相机中心,使物体的二维投影由图像中完全相同的像素组成。
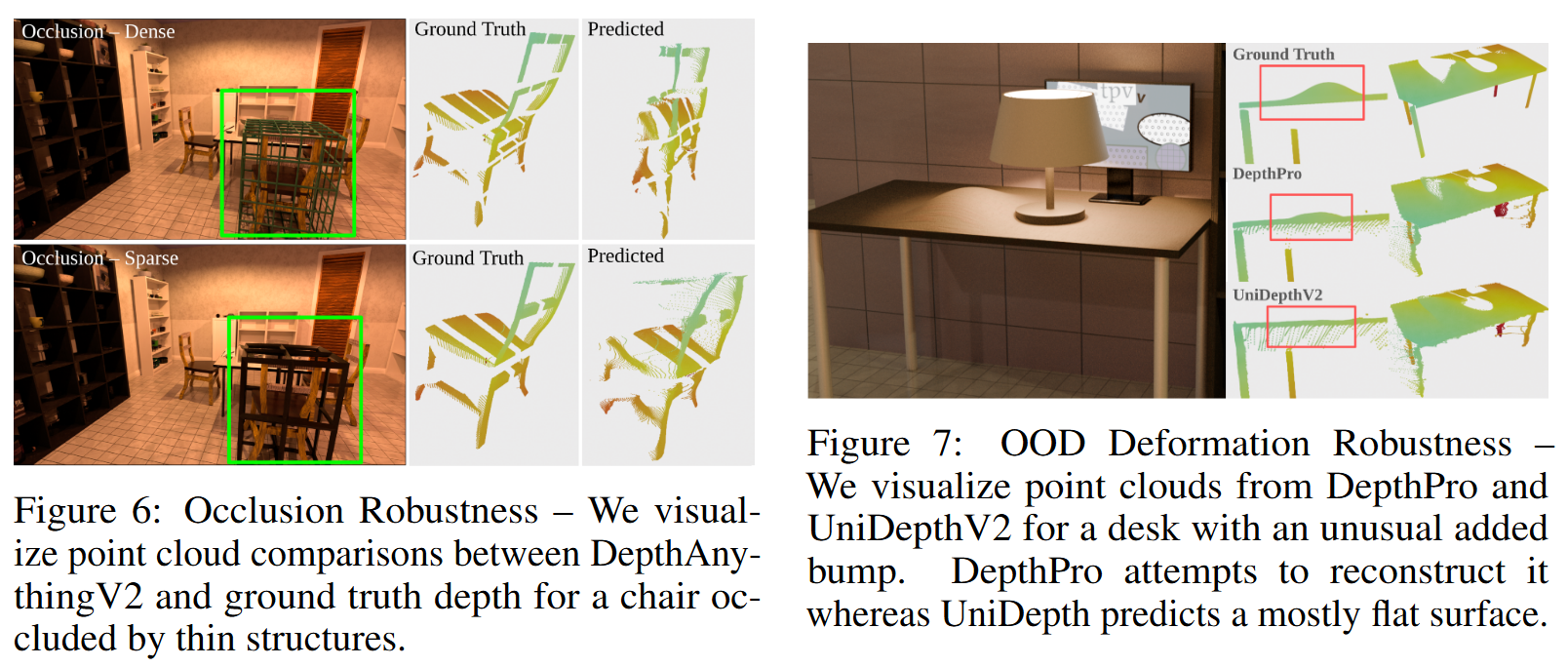
- 遮挡:在感兴趣的物体周围添加一个笼子形状的物体,改变线条的数量和粗细,产生10-40%的遮挡。
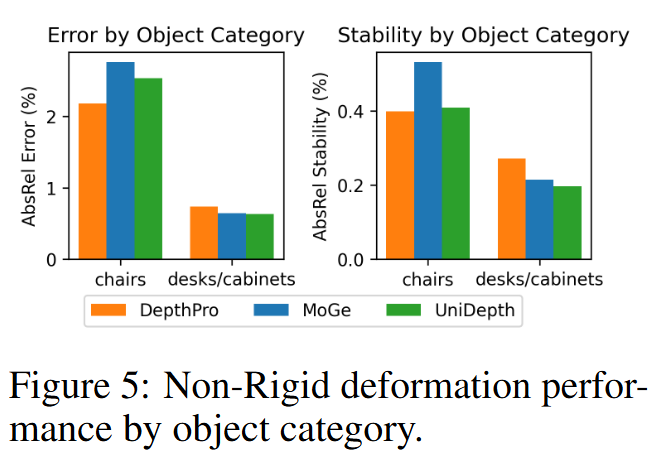
- 非刚性变形:以非刚性的方式使感兴趣的物体变形。有些是常见的,比如打开橱柜的门。有些是不寻常的,而且分布不均,比如形状扭曲的橱柜。
- 分布外的背景变换:将物体放置在一个不寻常的背景场景中,比如水下的椅子。物体相对于相机的姿态是相同的。
部分扰动,如光照变化和材料变化不会改变真实值,因此可以增强扰动来对模型的鲁棒性进行压力测试。而其他一些扰动会改变真实值,在这种情况下将扰动限制在小的邻域内,使得真实深度的变化不会那么剧烈。
仅评估不改变地面真实值的扰动的自洽性,以下两种特殊情况除外:(1) 相机滚动:它会对物体的深度图像进行SE(2)变换,即深度图像会发生变化,但仅限于旋转和平移。通过考虑这种旋转和平移来评估自洽性。(2)物体缩放:虽然物体与其背景几何体相比变大了,但相机中心会移动,使对象的2D投影保持不变,其深度图像也是如此。
评估指标
$\Delta(x_1,x_2)$ 是一个深度误差指标,计算两个深度图之间的差异。给定一个基本的场景和$N$个扰动,让$x_0$表示基本场景中模型的深度预测,$x_i,i=1,…,N$表示扰动场景的深度预测,$\hat{x}_i,i=0,…,N$ 表示对应的真实深度图,计算三个指标:
平均误差$\mu$:表示扰动场景加上基本场景与真实值之间误差的平均值
精度稳定性$\sigma$:基本场景和扰动场景深度误差的样本方差
自洽性$\mathcal{k}$:基本场景的预测和扰动下的预测之间的平均平方差
对于预测仿射不变深度的方法不计算自洽性,因为在没有真实值参考的情况下,放射不变深度的尺度和偏移是未知的,无法确定自洽性指标是否对尺度和偏移具有不变性。
评估方法
使用每个模型的默认推理流程,输出的深度图与数据集的分辨率保持一致,使用Marigold和MiDaS中的尺度偏移对齐的方法。在对一个感兴趣的物体进行评估时,只计算物体的深度值的对齐
分析
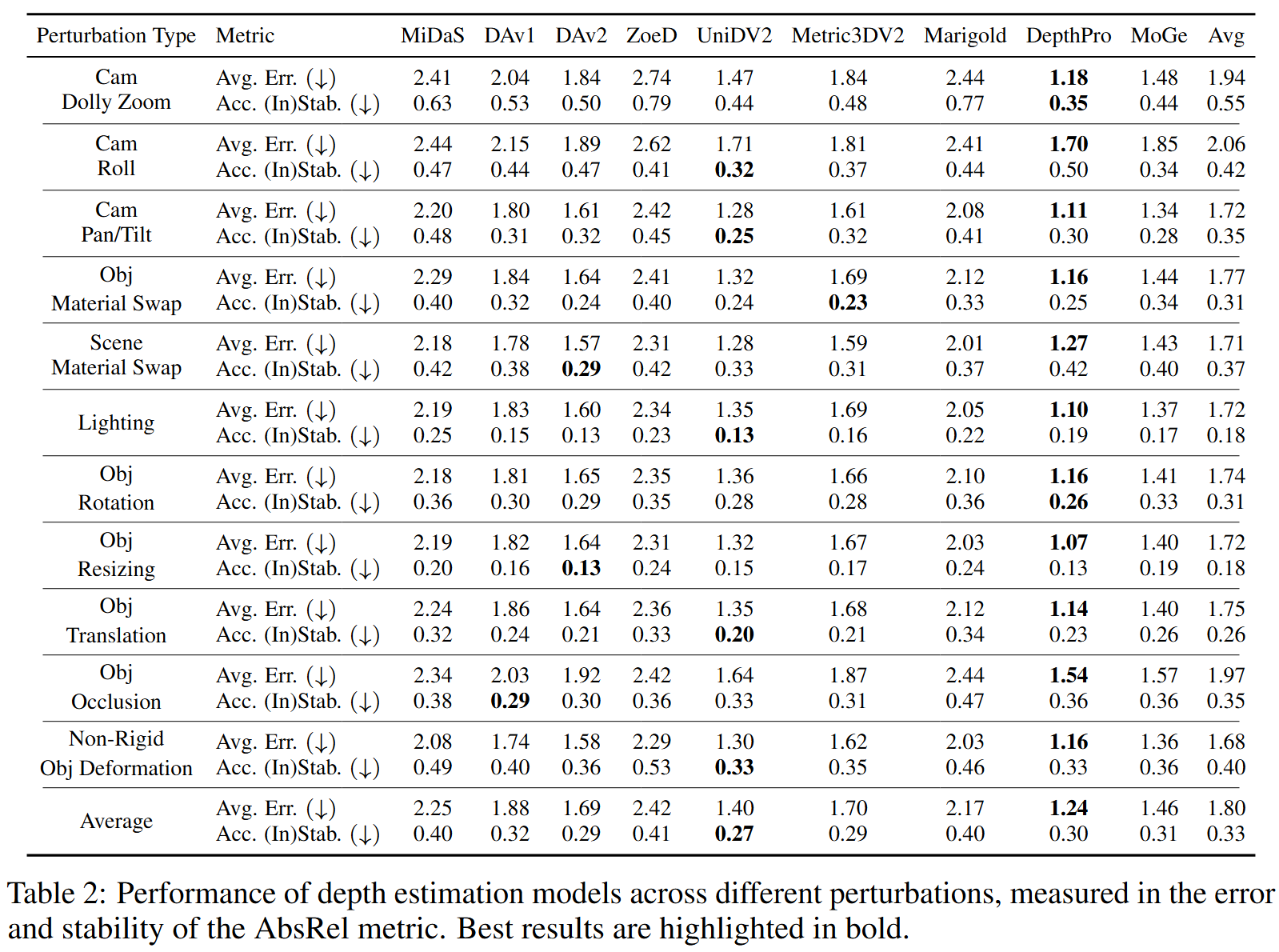
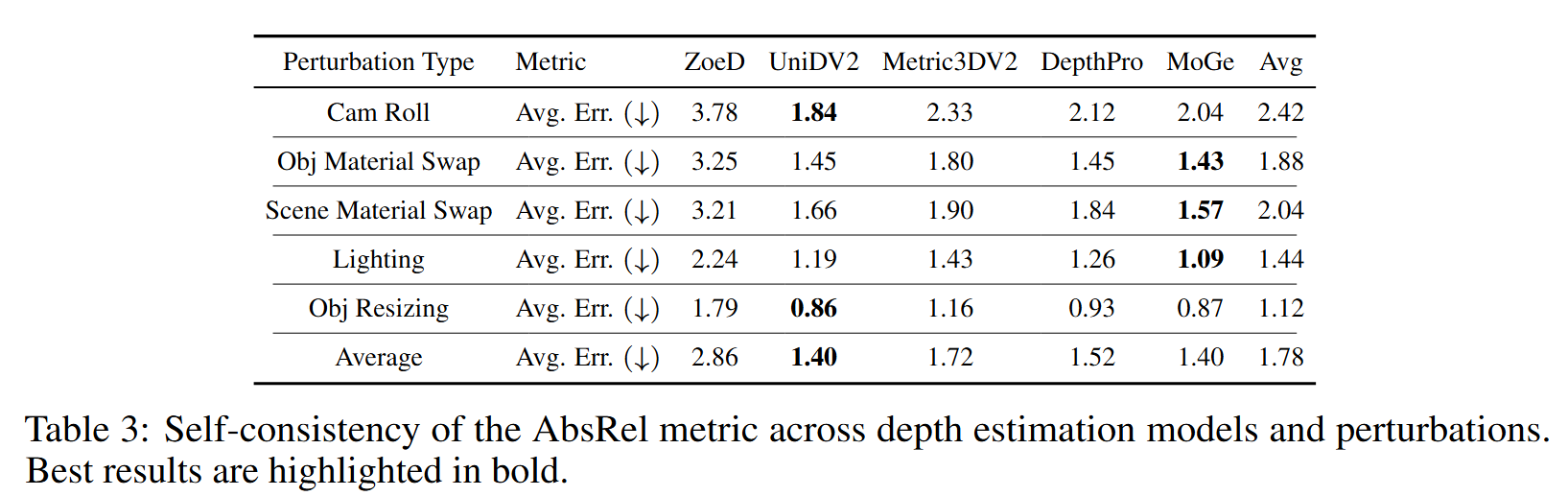

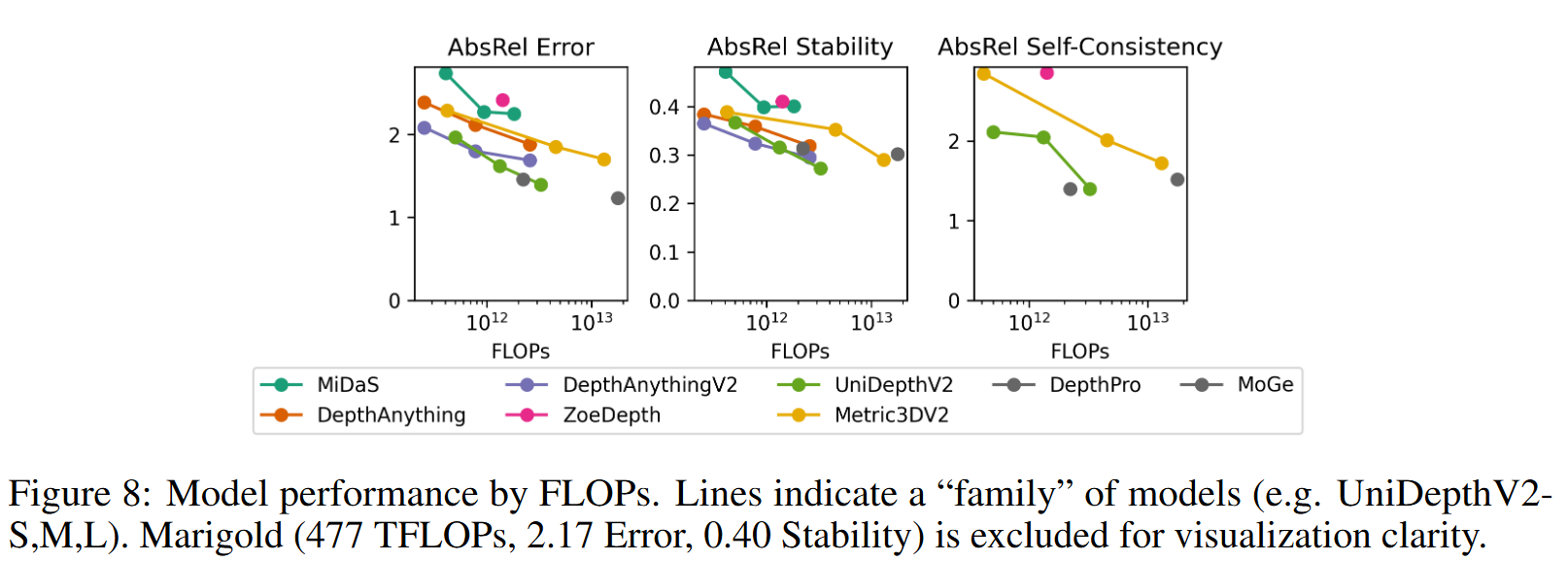
DepthPro与真值的误差最低,约为13%,在每种变体上都达到最低误差。
UniDepthV2和Metric3DV2具有最佳的稳定性结果。
在应用自洽性的尺度不变模型中,UniDepthV2得分最高,紧随其后的是MoGe。
尽管DepthPro可以最好地预测物体的详细深度图,但它对扰动的鲁棒性不如其他MDE模型。