Calibrating Panoramic Depth Estimation for Practical Localization and Mapping

摘要

从全景图像预测的精确深度能够作为许多下游任务的强大且轻量的输入。尽管全景图像能够捕捉周围环境的语义，但估计的深度仍然具有传统基于图像的深度估计方法的局限性：面对较大的领域偏移性能会下降，从二维观测中推断绝对值仍然是模糊的。通过利用整体视图，我们以自监督的方式减轻了这种影响，并在测试阶段对具有几何一致性的网络进行了微调。具体而言，我们从当前的深度预测构建一个三维点云，并将点云投影到不同的视角或对当前输入的图像进行拉伸来生成合成的全景图。然后我们最小化合成图像的三维结构预测的差异。

简介

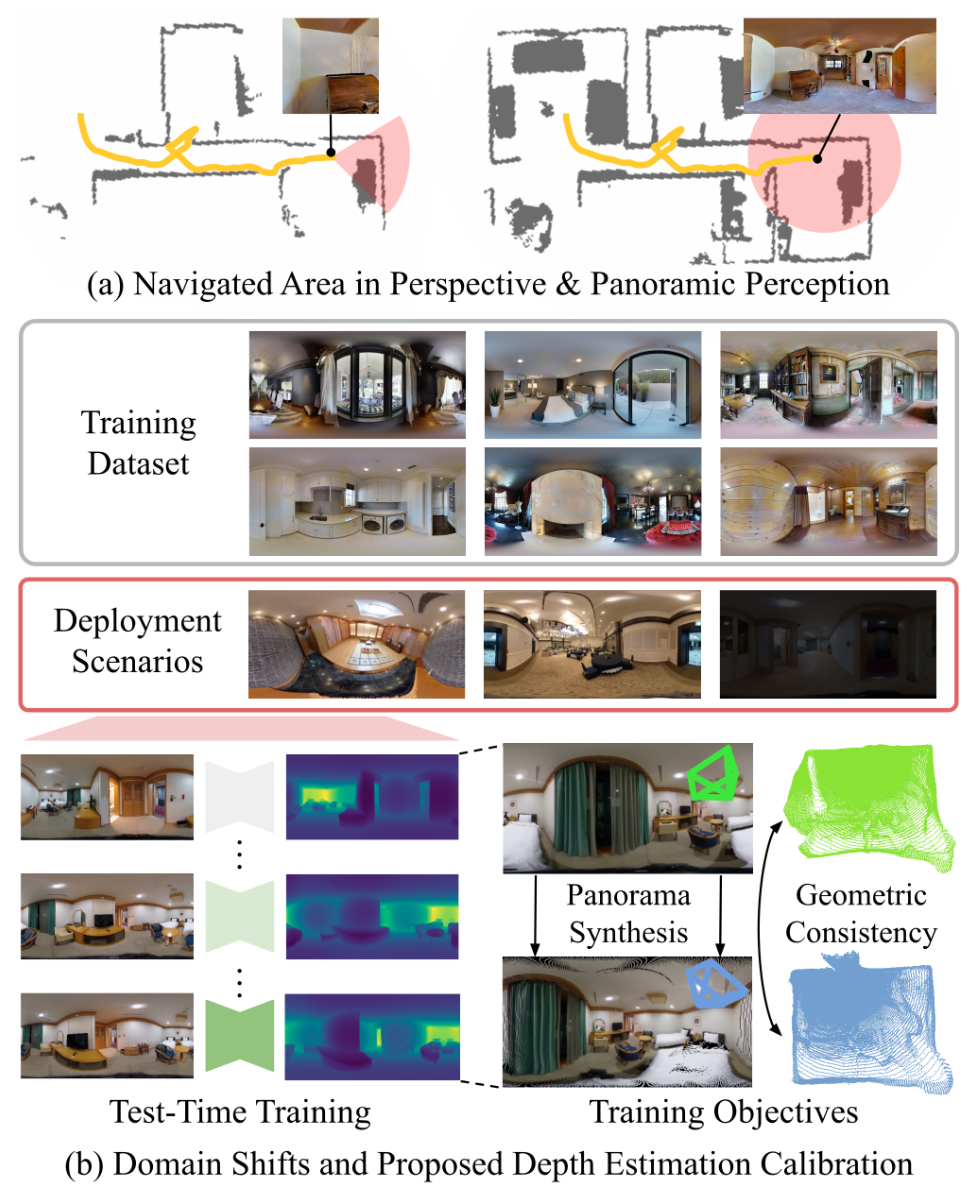
全景深度图的大视场角能够从单张图像中建模综合的三维语义。根据全景图像机器人导航能够观察到更大的区域，构建更加综合的地图。

现有的全景深度估计方法虽然能够预测高精度的深度图，但是在具有较大领域差距的没有见过的场景中性能会下降。虽然有很多方法用于非监督的领域适应，但他们主要考虑的是仿真到真实的差距最小化，且需要有标签的训练数据。

在本文中提出了一个快速且有效的全景深度估计的校准方法，主要包含两个关键组件。第一个是新视角合成和全景图拉伸之间几何一致性的训练目标。第二个是提出了轻量的数据增强，应对只有有限测试时间训练数据可用的离线场景。

方法

给定一个在源域$\mathcal{S}$上训练的全景深度估计网络$F_{\Theta}(\cdot)$，校准方案的目标是让网络在测试阶段自适应到一个新的，未见过的目标域$\mathcal{T}$。在线的情况，网络同步进行优化和评估。离线的情况，网络首先使用目标域的样本进行优化，然后用目标域样本的另一个集合进行评估。

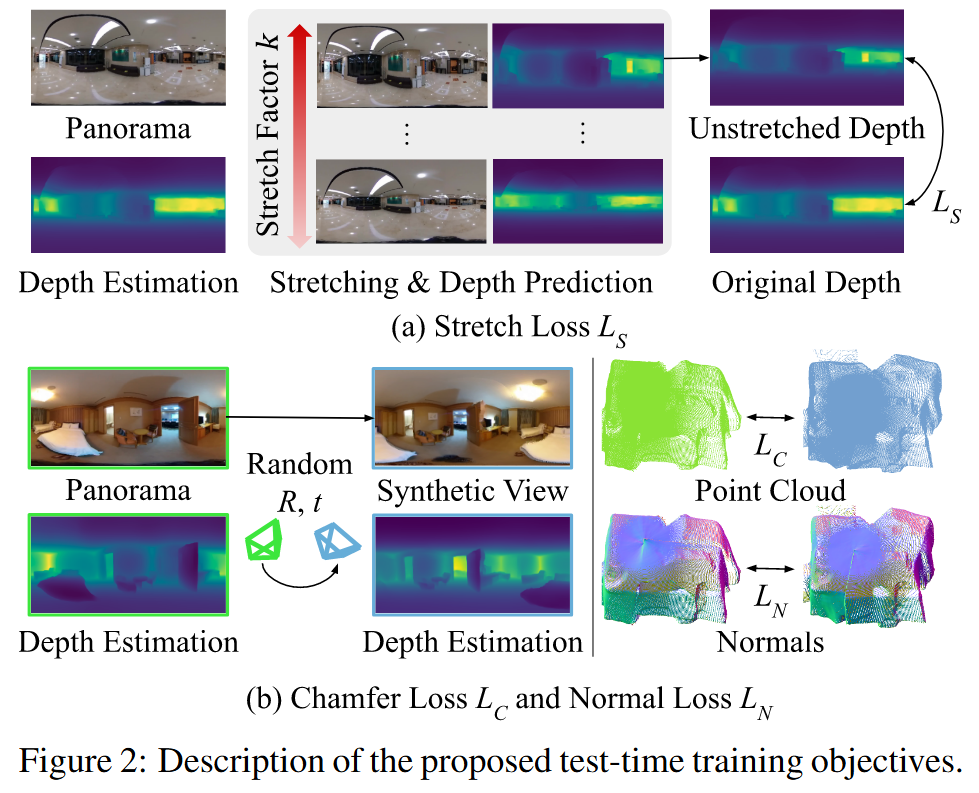
测试时间训练目标

给定一张全景图像$I\in \mathbb{R}^{H\times W \times 3}$，深度估计网络输出一个深度图$\hat{D}=F_{\Theta}(I)\in \mathbb{R}^{H \times W \times 1}$。目标函数如下

$$\mathcal{L}=\mathcal{L}_S+\mathcal{L}_C+\mathcal{L}_N$$

分别为拉伸损失，切角损失和发现损失

拉伸损失通过对不同的全景拉伸的深度预测施加一致性来解决全景深度预测中常出现的深度分布偏移。拉伸操作将全景图$I$ warp为另一个相同场景下的全景图，但是沿着$x,y$轴以参数$k$拉伸

$$\mathcal{S}^k_{img}(I)[u,v]=I[u,\frac{H}{\pi}\arctan(\frac{1}{k}\tan(\frac{\pi v}{H}))],$$

其中$I[u,v]$表示在坐标$(u,v)$处的颜色值，$\mathcal{S}^k_{img}(\cdot)$表示图像的第$k$次的拉伸函数。对应的深度图的的相同的操作如下

$$\mathcal{S}^k_{dpt}(D)[u,v]=\kappa(v)D[i,\frac{H}{\pi}\arctan(\frac{1}{k}\tan(\frac{\pi v}{H}))],$$

其中$\kappa(v)=\sqrt{k^2\sin^2(\pi v/H)+\cos^2(\pi v/H)}$，是由拉伸引起的深度值的变化的修正项。

拉伸损失迫使在大场景和小场景之间的深度预测具有一致性。大场景和小场景的区分是使用平均深度值的阈值$\delta_1$和$\delta_2$进行区分的。

$$\mathcal{L}_S = \begin{cases} \sum_{k \in \mathcal{K}_s} \left\| \hat{D} - S_{dpt}^{1/k} \left( F_{\Theta} \left( S_{k}^{img}(I) \right) \right) \right\|_2 & \text{if } \text{avg}(\hat{D}) < \delta_1, \\ \sum_{k \in \mathcal{K}_l} \left\| \hat{D} - S_{dpt}^{1/k} \left( F_{\Theta} \left( S_{k}^{img}(I) \right) \right) \right\|_2 & \text{if } \text{avg}(\hat{D}) > \delta_2, \\ 0 & \text{otherwise}. \end{cases}$$

其中$\text{avg}(\hat{D})$是深度图$\hat{D}=F_{\Theta}(I)$的像素级平均值，$\mathcal{K}_l={\sigma,\sigma^2}$, $\mathcal{K}_s={1/\sigma,1/\sigma^2}$是拉伸因子。具体实现时，$\delta_1=1,\delta_2=2.5,\sigma=0.8$

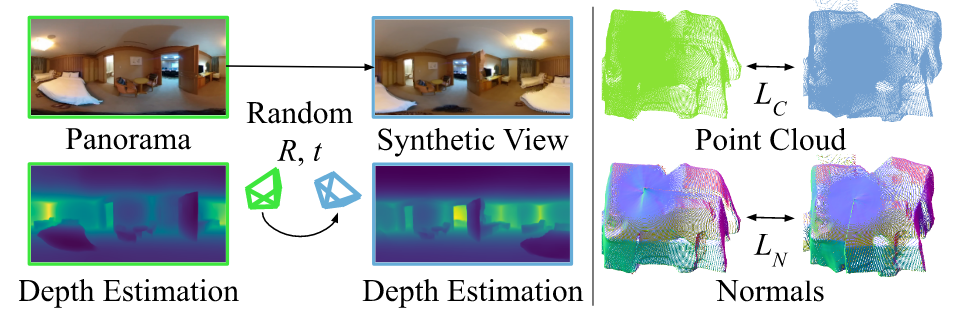
倒角和法线损失使深度预测在更精细的层面上具有几何一致性。在原始的视角上添加小随机姿态扰动来合成新视角，然后最小化合成视角和原视角之间的深度预测的差异。

倒角距离最小化不同姿态下深度预测之间的倒角距离，用$\mathcal{B}(D):\mathbb{R}^{H \times W \times 1} \rightarrow \mathbb{R}^{HW \times 3}$表示将每个像素的深度值$D[u,v]$投影到三维空间$D[u,v]*S[u,v]$中的点的反投影函数，其中$S[u,v]\in \mathbb{R}^3$是对应全景图坐标$(u,v)$的单位球上的点。让$\mathcal{W}(I,D;R,t)$表示warp函数，输出在随机姿态$R,t$下渲染的图像，则倒角损失计算为：

$$\mathcal{L}_C = \sum_{x \in \mathcal{B}(\hat{D})} \min_{y \in \mathcal{B}(D_{warp})} \left\| \tilde{R}x + \tilde{t} - y \right\|_2^2$$

其中$D_{\text{warp}}=F_{\Theta}(\mathcal{W}(I,\hat{D};\tilde{R},\tilde{t}))$是warp后图像的深度预测。

法线损失通过对齐深度图的法线向量来增加一层几何一致性。让$\mathcal{N}(\mathbf{x}:\mathbb{R}^3 \rightarrow \mathbb{R}^3)$表示法线预测函数，使用点$\mathbf{x}$周围的球查询来计算法线向量。法线损失计算为：

$$\mathcal{L}_N = \sum_{x \in \mathcal{B}(\hat{D})} \left( \tilde{R}N(x) \cdot \left( \tilde{R}x + \tilde{t} - \text{arg}\min_{y \in \mathcal{B}(D_{warp})} \left\| \tilde{R}x + \tilde{t} - y \right\|_2 \right) \right)^2$$

法线损失最小化原始深度图和warp后图像的深度图点的平面扫描之间的距离。

数据增强

对于离线自适应场景，只有少量的目标域数据可获得，因此使用数据增强策略来增加测试时间训练数据量。给定单张全景图像$I$和对应的深度预测$\hat{D}=F_{\Theta}(I)$，用于生成新的全景图的增强策略由下式给定：

$$\mathcal{A}(I, \hat{D}) = \begin{cases} \mathcal{W}(I, \hat{D}; \tilde{R}, \tilde{t}) & \text{if } \mathrm{avg}(\hat{D}) \in [\delta_1, \delta_2] \\ \mathcal{S}_{\mathrm{img}}^k(I) & \text{otherwise}, \end{cases}$$

其中$\tilde{R},\tilde{t}$是原点附近随机采样的位姿，如果$\text{avg}(\hat{D})>\delta_2$,$k$从$\mathcal{U}(\sigma^2,\sigma)$中随机采样，如果$\text{avg}(\hat{D})<\delta_1$,从$\mathcal{U}(1/\sigma,1/\sigma^2)$中随机采样。

应用

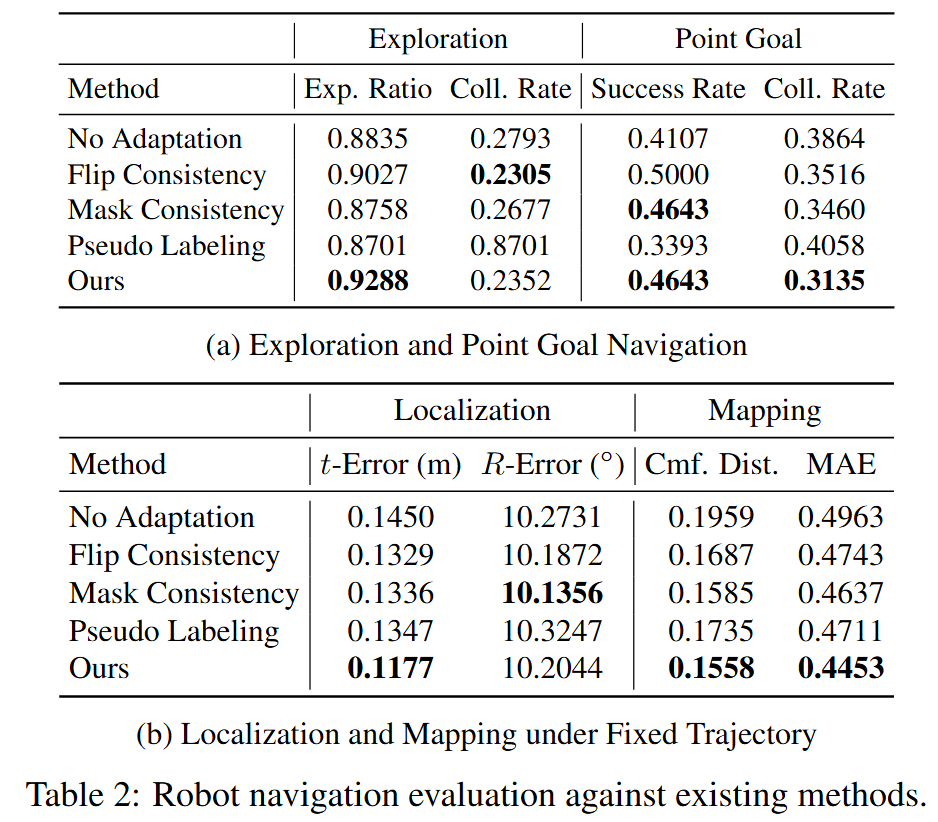
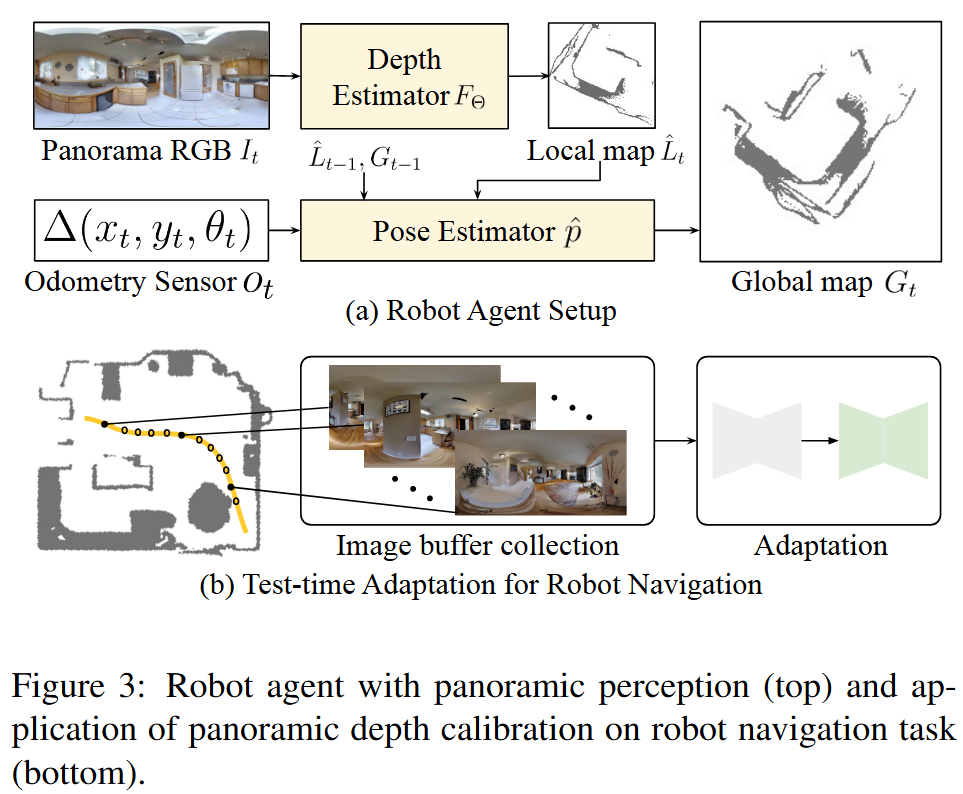
机器人定位

无地图视觉定位

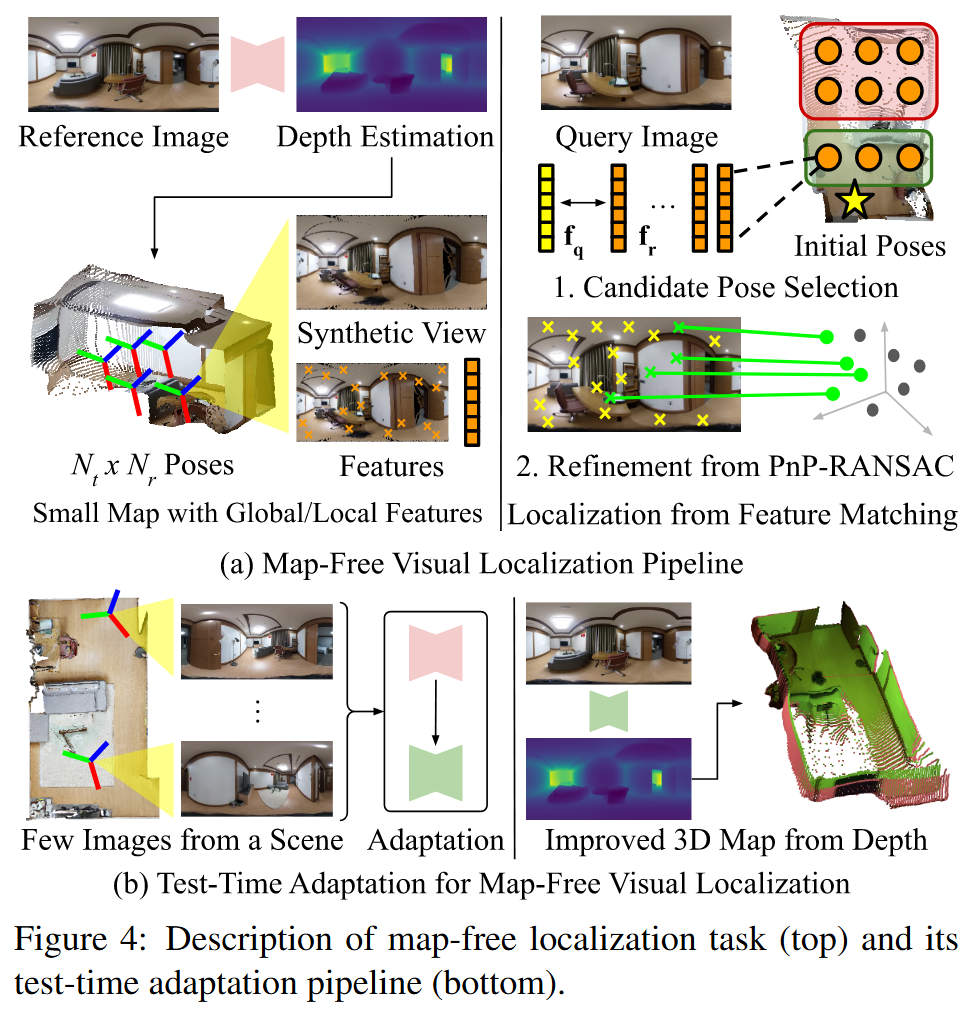
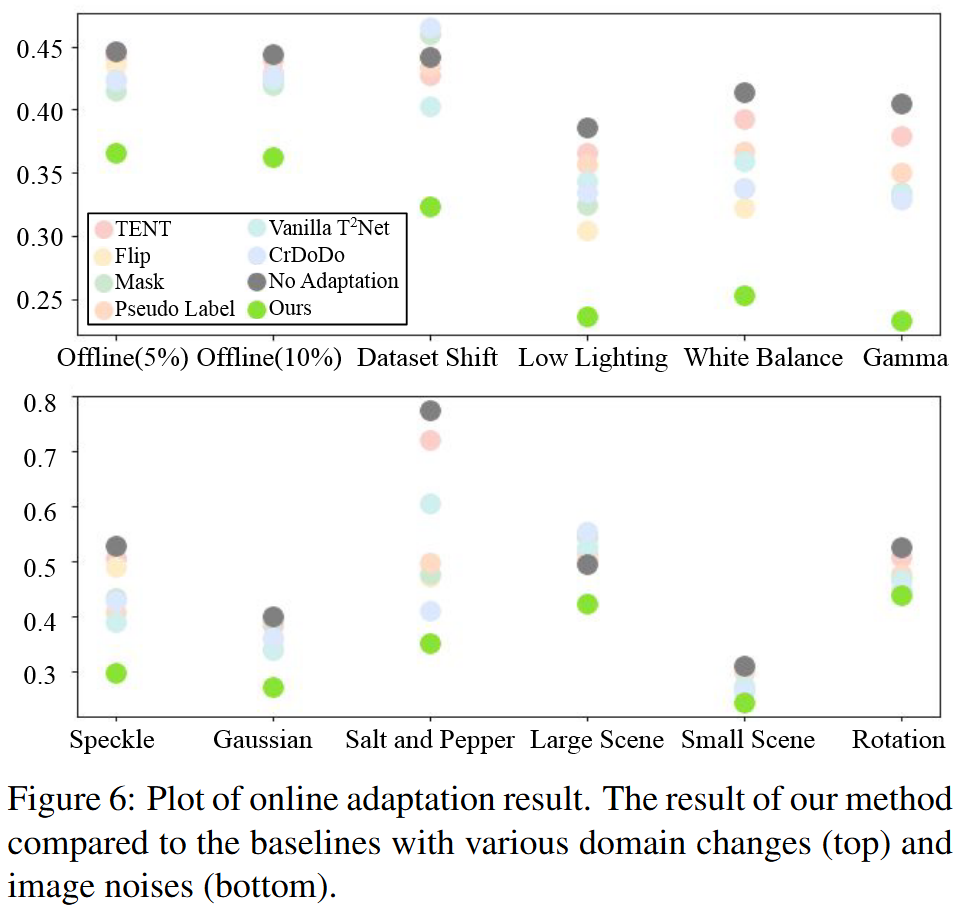
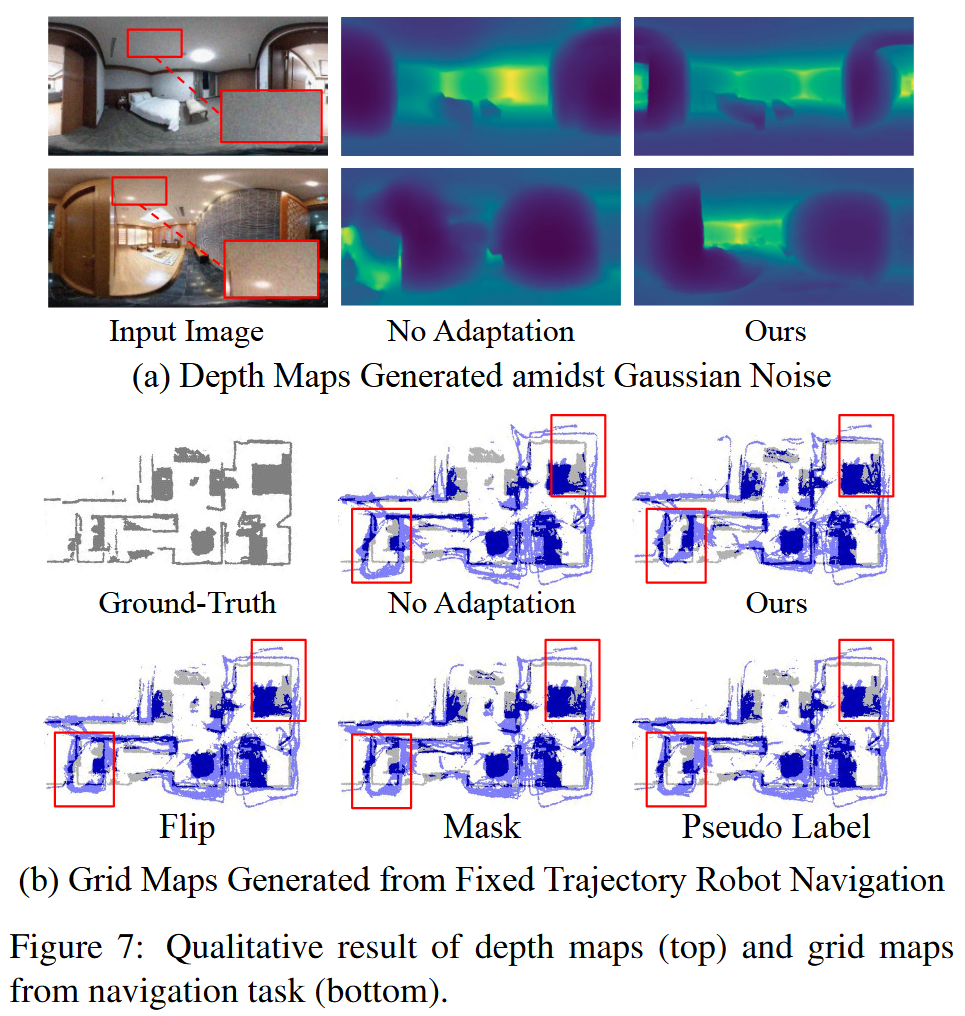
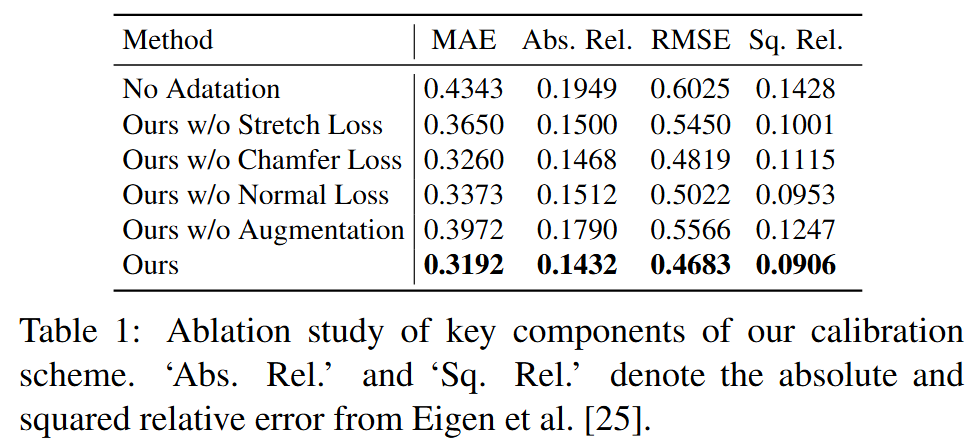
结果