Depth Anything 3: Recovering the Visual Space from Any Views
微信
支付宝
相关推荐
2025-04-10
VGGT: Visual Geometry Grounded Transformer
摘要三维计算机视觉通常被约束在单个任务中，因此我们提出了VGGT，一个前馈神经网络，直接推理场景的所有三维属性，包括相机参数，点云，深度图和三维点轨迹。同时该方法简单且效率高，可以在一秒内重建图像。 简介传统的三维重建任务采用视觉几何方法，但是会增加求解的复杂性和计算成本。DUSt3R等方法虽然能直接使用一个神经网络实现三维任务，但只能接受两个图像的输入，需要后处理来重建更多的图像。 VGGT不需要特定的网络，使用的是标准的transformer结构，在大规模公开数据集上训练。尽管存在潜在的冗余，但学习预测这些相互关联的3D属性可以提高整体准确性。在推理过程中，我们可以从单独预测的深度和相机参数中推导出点云，相比使用点云head可以得到更高的精度。 方法 问题定义和符号输入是$N$张图像$I_i \in \mathbb{R}^{3 \times H \times W}$ 的序列$(I_i)^N_{i=1}$，VGGT transofrmer将序列映射为对应的三维注释： f \left( (I_i)_{i=1}^N \right) = (\mathbf{g}_i, D_i,...
2024-12-08
DIFFERENTIABLE 3D GAUSSIAN SPLATTING
3D高斯的优势：非结构化、可微、利用快速α混合进行渲染、无需法线 世界坐标系下，高斯由三维协方差矩阵和点（均值）μ表示： G ( x ) \,=e^{-\frac{1} {2} ( x )^{T} \Sigma^{-1} ( x )} \tag{4}给定视角变换矩阵W，相机坐标系下的协方差矩阵为： \Sigma^{\prime}=J W \Sigma W^{T} J^{T} \tag{5}其中J是投影变换的仿射近似雅可比矩阵 协方差矩阵只有在半正定的时候才具有物理意义，而如果直接对协方差矩阵使用梯度下降优化，很难保证矩阵的合理性。 由于协方差矩阵是用来描述椭球的形状，因此可以用缩放矩阵S和旋转矩阵R来获得一个对应的协方差矩阵： \Sigma=R S S^{T} R^{T}\tag{6}OPTIMIZATION WITH ADAPTIVE DENSITY CONTROL OF 3D GAUSSIANSOptimization优化的参数：位置p，α，协方差矩阵，球谐函数系数 \mathcal{L}=( 1-\lambda)...
2024-12-08
DUSt3R: Geometric 3D Vision Made Easy
相关概念Pointmap将三维点的稠密二维场表示为pointmap $X \in\mathbb{R}^{W \times H \times3}$ ，对应分辨率为$W×H$ 的RGB图像 $I$，$X$描述了图像像素和三维场景点之间的一一对应关系。 假设每一条相机光线只会击中一个三维点，即忽略半透明表面的情况 Cameras and scene给定相机内参矩阵$K \in\mathbb{R}^{3 \times3}$ ，pointmap就能够根据给定的ground-truth 深度图$D \in\mathbb{R}^{W \times H}$ 获得： X_{i, j}=K^{-1} D_{i, j} \left[ i, j, 1 \right]^{\top}$X^{n,m}$表示相机$n$的pointmap $X^n$在相机$m$坐标系中的表示： X^{n, m}=P_{m} P_{n}^{-1} h \left( X^{n} \right) \tag{1}其中$P{m}, P{n} \in\mathbb{R}^{3 \times4}$ 是世界坐标系到相机坐标系的位姿，$h...
2024-12-08
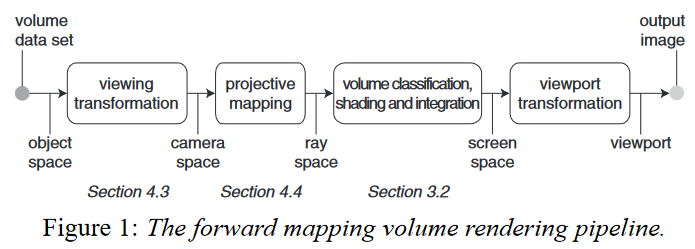
EWA Volume Splatting
elliptical Gaussian kernels 椭圆高斯核 Splatting algorithms interpret volume data as a set of particles that are absorbing and emitting light. 泼溅算法将体素数据解释为一组吸收和发射光的粒子。 Our method is based on a novel framework to compute the footprint function, which relies on the transformation of the volume data to so-called ray space. This transformation is equivalent to perspective projection. By using its local affine approximation at each voxel, we derive an analytic expression for the EWA footprint in...
2024-12-08
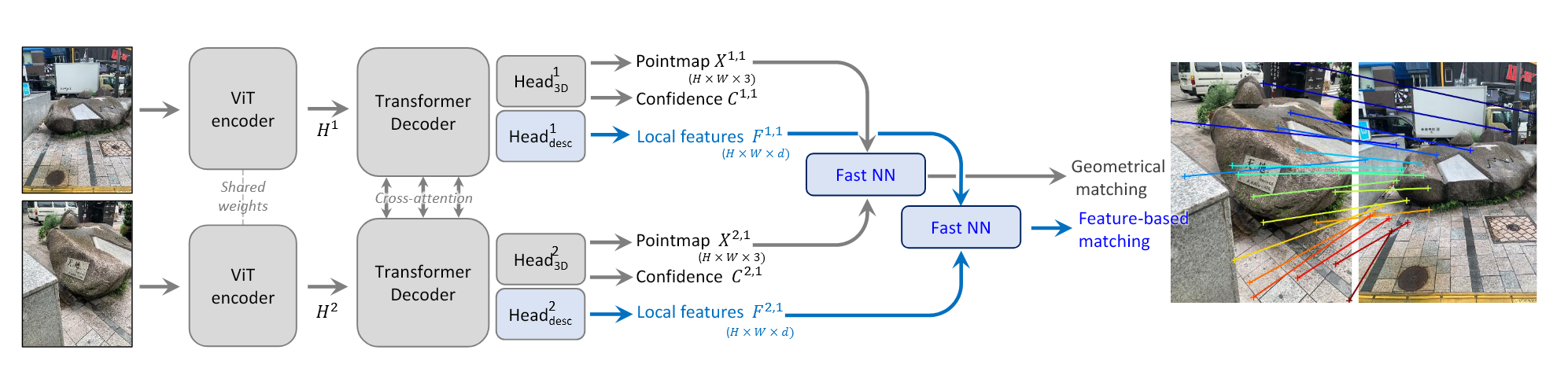
Grounding Image Matching in 3D with MASt3R
问题描述给定两张图像 $I^1$ 和 $I^2$ ，分别由未知参数的相机 $C^1$ 和 $C^2$ 采集，恢复出一组像素对应点 ${(i,j)}$ Method 由于gt pointmaps是metric的，所以为了得到metric的预测，将原本的nomalize的因子设置为 $z:= \hat{z}$ Matching prediction head and loss回归的方法固有地会受到噪声地影响，且DUSt3R没有显式地针对matching任务做训练。 Matching head D^{1}=\mathrm{H e a d}_{\mathrm{d e s c}}^{1} ( [ H^{1}, H^{\prime1} ] ), \tag{8} D^{2}=\mathrm{H e a d}_{\mathrm{d e s c}}^{2} ( [ H^{2}, H^{\prime2} ] ). \tag{9}Head是一个简单的两层MLP以及非线性GELU激活函数，最后，将每个局部feature 归一化。 Matching objective 一张图像中的每一个local...
2024-12-08
Mip-Splatting: Alias-free 3D Gaussian Splatting
3DGS在改变采样率或者改变焦距和相机距离时，会存在严重的膨胀效应和高频伪影 采样理论（奈奎斯特-香农采样理论）对连续信号的采样频率至少是最大频率的两倍，所以在采样之前要对信号施加滤波。 3DGS中的Dilation操作为了防止投影的2DGS小于一个像素，所以投影的2DGS进行了膨胀操作： {\mathcal G}_{k}^{2 D} ( \mathbf x )=e^{-{\frac{1} {2}} ( \mathbf x-\mathbf p_{k} )^{T}} ( \mathbf\Sigma_{k}^{2 D}+s \, \mathbf I )^{-1} \, ( \mathbf x-\mathbf p_{k} ) \tag{5}Sensitivity to Sampling Rate 对于Zoom-out，原本的object在像素中的占比缩小了，所以为了要膨胀到一个像素的大小，施加的二维膨胀相较于原来更大 对于Zoom-out，原本的object在像素中的占比变大，所以膨胀到一个像素大小所需的二维膨胀就更小 it leads to erosion effects...
最新文章
