DUSt3R: Geometric 3D Vision Made Easy

Method

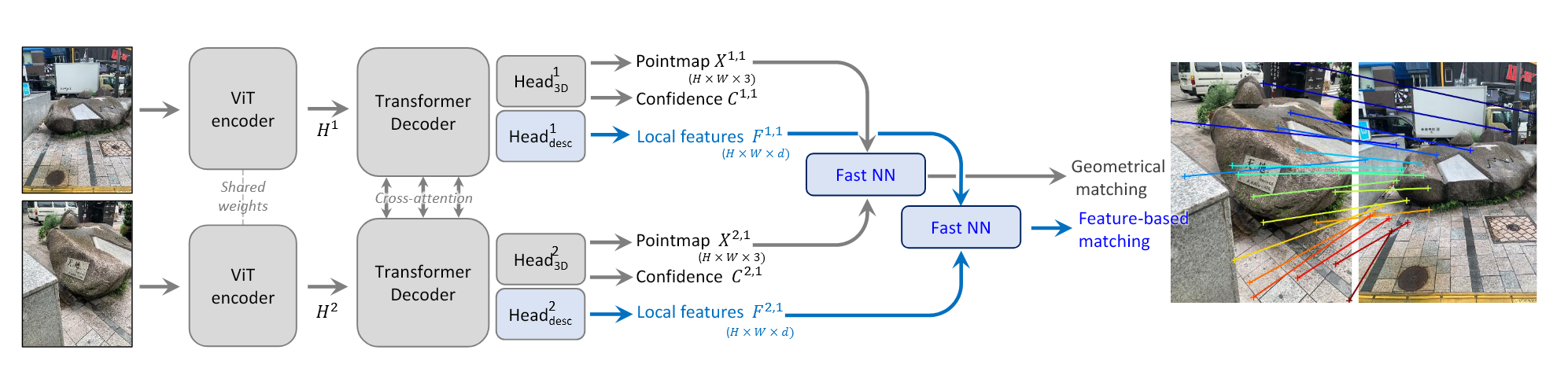
input：两张RGB图像 $I^{1}, I^{2} \in\mathbb{R}^{W \times H \times3}$ ，输出对应的两张pointmap $X^{1, 1}, X^{2, 1} \in\mathbb{R}^{W \times H \times3}$ 和置信度图 $C^{1, 1}, C^{2, 1} \in\mathbb{R}^{W \times H}$ 。pointmap都是在 $I^{1}$ 的坐标系下表示的。

Network architecture

Dust3r1

输入图像通过相同共享权重的ViT encoder得到两个token表示$F^1$ , $F^2$ :

$F^{1}=\mathrm{E n c o d e r} ( I^{1} ), F^{2}=\mathrm{E n c o d e r} ( I^{2} ).$

在decoder内分别进行cross-attention 和self-attention操作，self-attention中每一个视角中的每一个token和相同视角下的其他token进行操作，cross-attention中一个视角下的一个token和另一个视角下的所有token进行操作。最后输入到MLP中。

decoder有$B$ 个blocks，$\mathrm{D e c o d e r B l o c k}_{i}^{v} ( G^{1}, G^{2} )$ 表示分支 $v$ 中的第 $i$ 个block，其中 $G^1,G^2$ 表示输入的tokens，则有：

$G_{i}^{1}=\mathrm{D e c o d e r B l o c k}_{i}^{1} \left( G_{i-1}^{1}, G_{i-1}^{2} \right) \\ G_{i}^{2}=\mathrm{D e c o d e r B l o c k}_{i}^{2} \left( G_{i-1}^{2}, G_{i-1}^{1} \right), \\$

最终每一个分支的decoder token集合分别输入到 regression head中，得到pointmap和置信度图：

$X^{1, 1}, \hat{C}^{1, 1}=\mathrm{H e a d}^{1} \left( G_{0}^{1}, \ldots, G_{B}^{1} \right),\\ X^{2, 1}, C^{2, 1}=\mathrm{H e a d}^{2} \left( G_{0}^{2}, \ldots, G_{B}^{2} \right).$

输出的pointmap按道理没有尺度约束，因此尺度因子不可知，但可以在训练的时候让网络从训练集中学习到具有几何一致性的pointmap

Training Objective

3D Regression loss

设根据公式（1）得到的gt pointmap为 ${\bar{X}}^{1, 1}$ 和 ${\bar{X}}^{2, 1}$ ,regression loss为：

$\ell_{\mathrm{r e g r}} ( v, i )=\left\| {\frac{1} {z}} X_{i}^{v, 1}-{\frac{1} {\bar{z}}} \bar{X}_{i}^{v, 1} \right\|. \tag{2}$

（只针对valid pixel）

为了解决scale ambiguity的问题，将prediction 和gt都进行归一化，缩放因子分别为 $z \,=\, \mathrm{n o r m} ( X^{1, 1}, X^{2, 1} )$ 和 $\bar{z} \,=\, \mathrm{n o r m} ( \bar{X}^{1, 1}, \bar{X}^{2, 1} )$ ,表示所有valid points到原点的平均距离：

$\operatorname{n o r m} ( X^{1}, X^{2} )={\frac{1} {| {\mathcal{D}}^{1} |+| {\mathcal{D}}^{2} |}} \sum_{v \in\{1, 2 \}} \sum_{i \in{\mathcal{D}}^{v}} \left\| X_{i}^{v} \right\|.\tag{3}$

Confidence-aware loss

在现实情况下，在天空或者半透明物体上可能会存在难以定义的三维点，因此同时也对每一个像素定义一个分数来表示网络对该像素的置信度，最终的训练目标是在valid pixels上的 confidence-weighted regression loss：

${\cal L}_{\mathrm{c o n f}}=\sum_{v \in\{1, 2 \}} \sum_{i \in{\cal D}^{v}} C_{i}^{v, 1} \ell_{\mathrm{r e g r}} ( v, i )-\alpha\operatorname{l o g} C_{i}^{v, 1},\tag{4}$ $C_{i}^{v, 1} \,=\, 1+\operatorname{e x p} c_{i}^{v, 1} \, \gg\, 0, c_{i}^{v, 1} \in\mathbb{R}$

Dust3r2

Downstream Applications

Point matching

两张图像中点的对应关系表示为：

$\mathcal{M}_{1, 2}=\{( a, b ) \mid a=\mathrm{N N}^{1, 2} ( b ) ~~ and ~~ b = NN^{2,1}(a)\}\\ \operatorname{w i t h} \operatorname{N N}^{n, m} ( a )=\underset{b \in\{0, \ldots, W H \}} {\operatorname{a r g} \operatorname* {m i n}} \left\| X_{b}^{n, 1}-X_{a}^{m, 1} \right\|.$

Recovering intrinsics

pointmap $X^{1,1}$ 是在图像 $I^1$ 的坐标系中，若假设principal point近似在中心，像素是方形的，则只需要估计焦距 $f^{*}_1$ :

$f_{1}^{*}=\underset{f_{1}} {\operatorname{a r g \, m i n}} \sum_{i=0}^{W} \sum_{j=0}^{H} C_{i, j}^{1, 1} \left\| ( i^{\prime}, j^{\prime} )-f_{1} \frac{( X_{i, j, 0}^{1, 1}, X_{i, j, 1}^{1, 1} )} {X_{i, j, 2}^{1, 1}} \right\|,$

其中

$i^{\prime}=i-\frac{W} {2}~~~ and ~~~j^{\prime}=j-\frac{H} {2}$

Relative pose estimation

一种方法是用上述方法恢复内参，然后估计对极矩阵恢复相对位姿

另一种方法是用 Procrustes alignment 直接比较pointmap得到相对位姿

$P^{*}=\sigma^{*} [ R^{*} | t^{*} ]:$ $P^{*}=\underset{\sigma, R, t} {\operatorname{a r g \, m i n}} \sum_{i} C_{i}^{1, 1} C_{i}^{1, 2} \left\| \sigma( R X_{i}^{1, 1}+t )-X_{i}^{1, 2} \right\|^{2},$

更加鲁棒的方法为RANSAC、PnP

Absolute pose estimation（Visual localization）

一种方法是让 $I^Q$ 表示 query image ， $I^B$ （其2D-3D的对应关系是可获得的）表示reference image。首先 $I^Q$ 的内参可以从 $X^Q$ 得到，然后可以对 $I^Q$ 和 $I^B$ 之间的二维像素对应关系运行PnP-RANSAC，从而得到 $I^Q$ 的2D-3D对应关系。

另一种方法是获得两个图像的相对位姿，然后根据 $X^{B,B}$ 和 $I^B$ 的gt pointmap之间的尺度将这个位姿转换到世界坐标系下。

Global Alignment

所构建的网络只能够处理图像对，因此需要进行快速简单的后处理来构建更大的场景，使得更多预测的pointmaps能够统一到同一个三维空间当中。

Pairwise graph

给定一个图像集 ${I^{1}, I^{2}, \ldots, I^{N} } $ ，首先构建一个连通图 ${\mathcal{G}}=( {\mathcal{V}}, {\mathcal{E}} )$ ,$N$ 张图像构成了顶点 $\mathcal{V}$ ,每一条边 $e \,=\, ( n, m ) \, \in\, \mathcal{E}$ 表示了图像 $I^n$ 和 $I^m$ 之间共有的视觉内容,然后通过现有的图像检索方法或者将所有图像对通过网络计算所有图像对的平均置信度，评估重叠的部分，从而滤除掉低置信度的图像对。

Global optimization

使用连通图 $ \mathcal{G} $ 对所有相机 $n=1…N$ 恢复全局对齐的pointmap ${\chi^{n} \in\mathbb{R}^{W \times H \times3} } $，首先预测每一个图像对的pointmaps 和对应的置信度图。为了表示方便，定义 $ X^{n, e} :=X^{n, n}\quad and \quad X^{m, e} :=X^{m, n} $ ，为了将所有图像对的预测都在同一个坐标系下进行表示，所以引入每一个图像对的 pairwise pose $ P_{e} \in \mathbb{R}^{3 \times 4} $ 和 scaling $ {\sigma}_e > 0 $，则对应的优化问题描述为：

$\chi^{*}=\underset{\chi, P, \sigma} {\operatorname{a r g \, m i n}} \sum_{e \in\mathcal{E}} \sum_{v \in e} \sum_{i=1}^{H W} C_{i}^{v, e} \| \chi_{i}^{v}-\sigma_{e} P_{e} X_{i}^{v, e} \| \,.\tag{5}$

其思想就是给定一个图像对，采用相同的刚性变换应当要把两个pointmaps 和世界坐标系下的pointmaps相对齐，为了避免陷入局部最优，对任意图像对，设定

${\prod}_{e}{\sigma}_{e}=1$