摘要

虽然当前的深度基础模型展现出了强大的泛化能力，但对于不同的相机类型要获得精确的绝对深度仍然是一个具有挑战性的问题，尤其是对于大视场角的相机，例如鱼眼和360度相机。

提出了一个零样本的的绝对深度估计框架Depth Any Camera（DAC），能够拓展基于透视训练的模型，处理不同视场角的相机。DAC只在透视图像上进行训练，但是能无缝地泛化到鱼眼和全景相机，不需要特定的训练数据。

方法：使用了等矩形投影（ERP）作为统一的图像表达，关键组件包括一个俯仰感知的图像到ERP地转换，一个视场角对齐操作以及多分辨率地数据增强。

简介

早期的基于深度学习的方法依赖于在单个数据及和深度传感器上的监督学习，由于尺度和深度的模糊性，单目深度估计仍然具有挑战性。

拓展训练数据或者使用自监督方法能够增强鲁棒性，但这些方法由于自监督的模糊性，会产生不一致性，或受到动态物体的影响。

近期的方法，例如MiDaS，使用了大规模数据进行三维的监督，但是其得到的是相对深度而不是绝对深度。

近期的一些方法解决了零样本的绝对深度估计问题，解决由于不同的相机内参带来的不一致的尺度的问题，但是这些方法不能够解决大视场角相机的图像预测问题。

depthanycamera-1

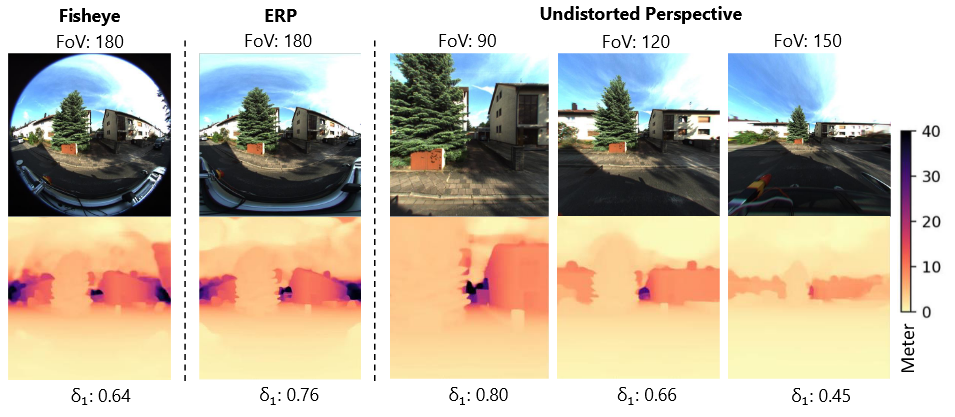
在任意视场角相机上达到零样本的深度泛化存在几大挑战：选择一个统一的相机模型来表示不同的视场角；有效地使用透视训练数据集以泛化至大视场角相机地数据空间；管理由不同视场角引起的统一空间中不同的训练图像大小；解决训练和测试阶段之间分辨率地不一致的问题

depthanycamera-2

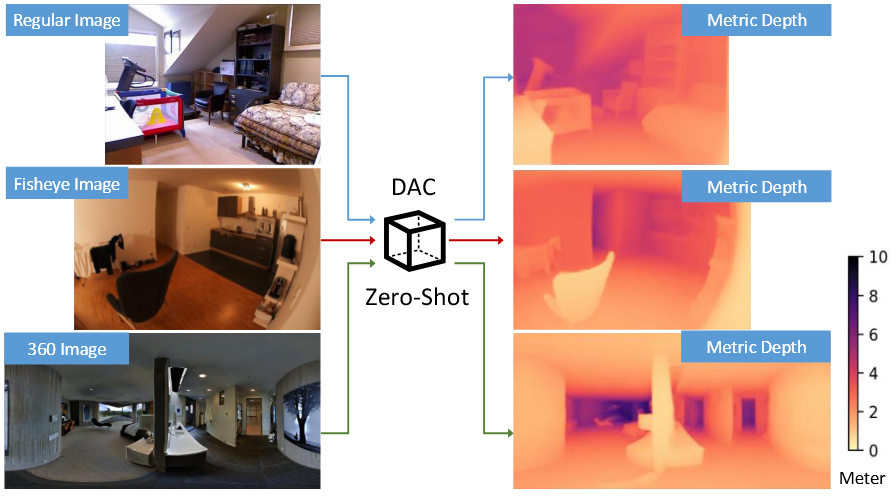
符号和准备工作

深度缩放操作

depthanycamera-3

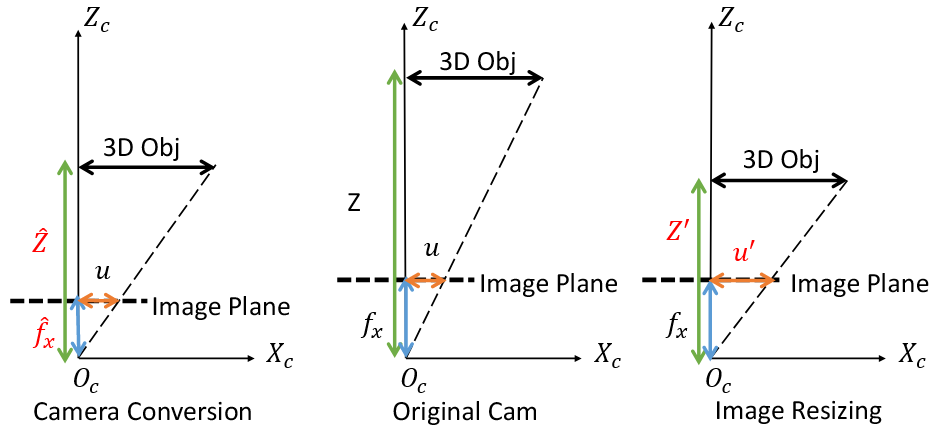
图像中物体的二维尺寸是由其三维的维度$X$，深度$Z$和相机的焦距$f_s$决定的。

将透视相机模型转换到标准空间模型中，需要按比例缩放深度值$\hat{Z} = \frac{\hat{f}_x Z}{f_x}$

当相机模型固定，但是图象被resize到$u’$，那么相当于在不同的距离观察相同的三维物体，也需要对深度值进行缩放$Z’=\frac{uZ}{u’}$

等矩形投影ERP

等矩形投影式基于球面相机模型的一种图像表示，每一个像素都对应于特定的纬度$\lambda$和经度$\phi$。一个完整的ERP空间

跨越纬度180°，经度360°，使其能够处理不同视场角的相机。ERP图像的高度是定义ERP空间所需的唯一参数。

从标准图像到ERP图像之间的转换使用Gnomonic投影转换，其提供了归一化图像坐标$(x_t,y_t)$和球面坐标$(\lambda,\phi)$之间的闭合映射，假设切平面以一个单位球的$(\lambda_c,\phi_c)$为中心。

$x_t = \frac{\cos \phi \sin (\lambda - \lambda_c)}{\cos c} \tag{1}$ $y_t = \frac{\cos \phi_c \sin \phi - \sin \phi_c \cos \phi \cos (\lambda - \lambda_c)}{\cos c} \tag{2}$

其中$c$是点$(x_t,y_t)$到投影中心的角距离，用下式给出：

$\cos c = \sin \phi_c \sin \phi + \cos \phi_c \cos \phi \cos (\lambda - \lambda_c) \quad (3)$

方法：Depth Any Camera

depthanycamera-0

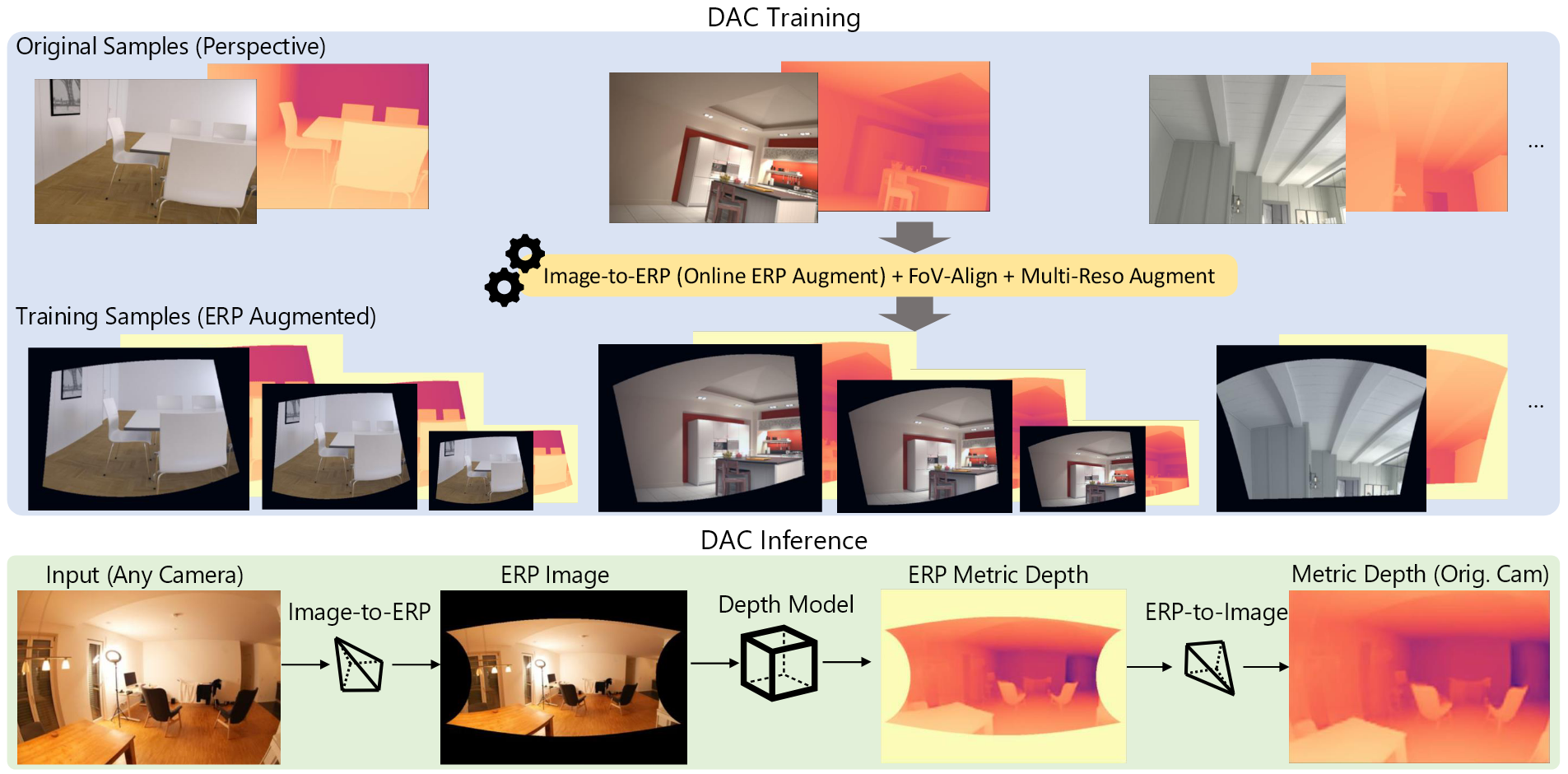
来自不同相机类型和视场角的图像转换到一个标准的ERP空间。在训练时，使用广泛的透视图像数据集，将他们转换为更小的ERP patches进行充分学习。测试时，大视场角的图像也相似地转换到标准的ERP空间，使得训练好的模型能够预测一致的绝对深度值。

俯仰感知的图像到ERP转换

假设ERP空间的高为$H_E$，宽度$W_E=2H_E$，图像的中心位于纬度$\lambda_c$，经度$\phi_c$，目标ERP patch的尺寸为$H_e \times W_e$，ERP patch的坐标$(u_e,v_e)$可以用以下公式映射到球面坐标系：

$\phi = \frac{2\pi W_e}{W_E} \left(u_e - \frac{W_e}{2}\right) + \phi_c \tag{4}$ $\lambda = \frac{\pi H_e}{H_E} \left(v_e - \frac{H_e}{2}\right) + \lambda_c \tag{5}$

使用公式1和2中的Gnomonic几何，可以在与单位球接触的切平面中获得对应的归一化的图像坐标$(x_t,y_t,1)$。为了将这个坐标映射到实际的图像坐标$(u,v)$，根据给定的相机参数应用失真和投影函数

$\begin{align*} (x_d, y_d) &= f_d(x, y, D_c) && \text{(6)} \\ (u, v) &= f_p(x_d, y_d, K_c) && \text{(7)} \end{align*}$

中$f_d$是失真函数，失真参数为$D_c$，$f_p$是以内参$K_c$为参数的投影函数。如果输入图像没有失真，可以直接对$(x_t,y_t)$应用投影函数

depthanycamera-4

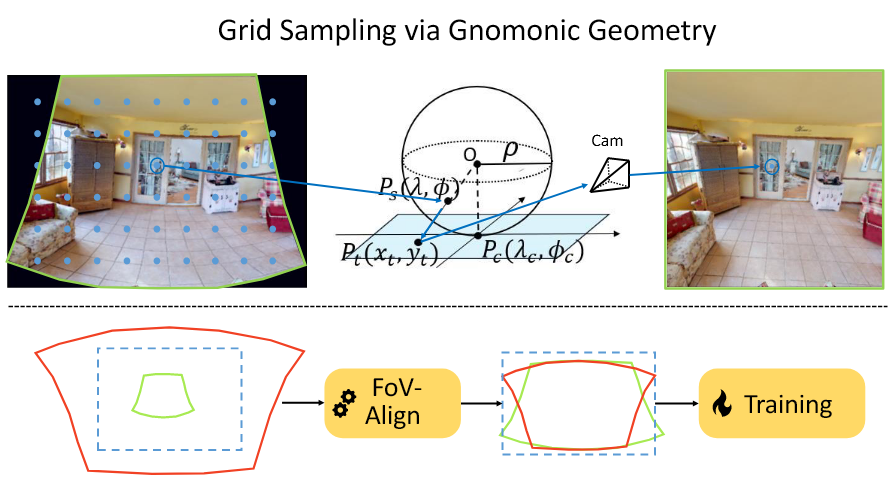
通过目标ERP patch中的统一的采样网格点，每一个网格点都能够直接映射到输入图像对应的位置。实际上，ERP patch中的每个网格点是映射到输入图像的特定浮点位置，实际的值是通过相邻像素插值获得的。

ERP转换的优势是具有相机的俯仰感知，当相机的方向是可获得的或者能够估计，那么透视的数据就能够被投影到ERP空间的不同纬度，能够模拟那些只有大视场角相机能够看到的区域。通过对$\lambda_c$引入噪声，就能够很简单地进行俯仰角的增强，产生不同形状的ERP patches。

另一个优势是，在透视图像中的增强操作可以无缝地在ERP空间中进行应用，只需要在归一化的图像坐标上进行增强就行

$\begin{bmatrix} x_t' \\ y_t' \end{bmatrix} = s_\sigma \begin{bmatrix} R_\sigma & T_\sigma \end{bmatrix} \begin{bmatrix} x_t \\ y_t \end{bmatrix} \tag{8}$

其中$s_\sigma$是尺度因子，$R_\sigma$是二维旋转矩阵，$T_\sigma$是二维位移向量。若使用缩放增强，真实的深度值也需要进行缩放保证尺度一致性。