摘要

由于系统性的测量偏差，例如密度、感知模式和扫描范围，当前方法在现实世界的应用范围有限。

学习联合表示的输入模式对偏差敏感。

设计了深度提示模块，根据传感器类型或场景配置的新深度分布获得希望的特征表示。

通过将这个模块嵌入基本的单目深度估计模型，可以解决深度扫描范围的限制，提供绝对的带尺度的深度图。

简介

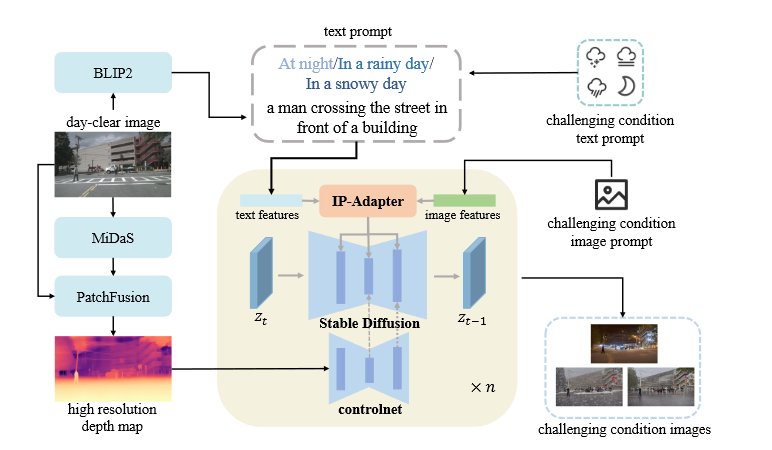
目标是构建一个传感器不可知的深度估计模型，能够在各种主动深度传感器上工作。深度提示首先编码稀疏的深度信息，并将其和图像特征进行融合构建一个逐像素的亲和力图。最后对亲和力图和最初的深度图进行细化操作。采用偏差调优技术，只需要对0.1%的模型参数进行微调。

Prompt Engineering

Prompt engineering是指设计特定的模板，指导模型以结构化的格式填充丢失的信息或者在给定输入的情况下生成有效的响应。

方法

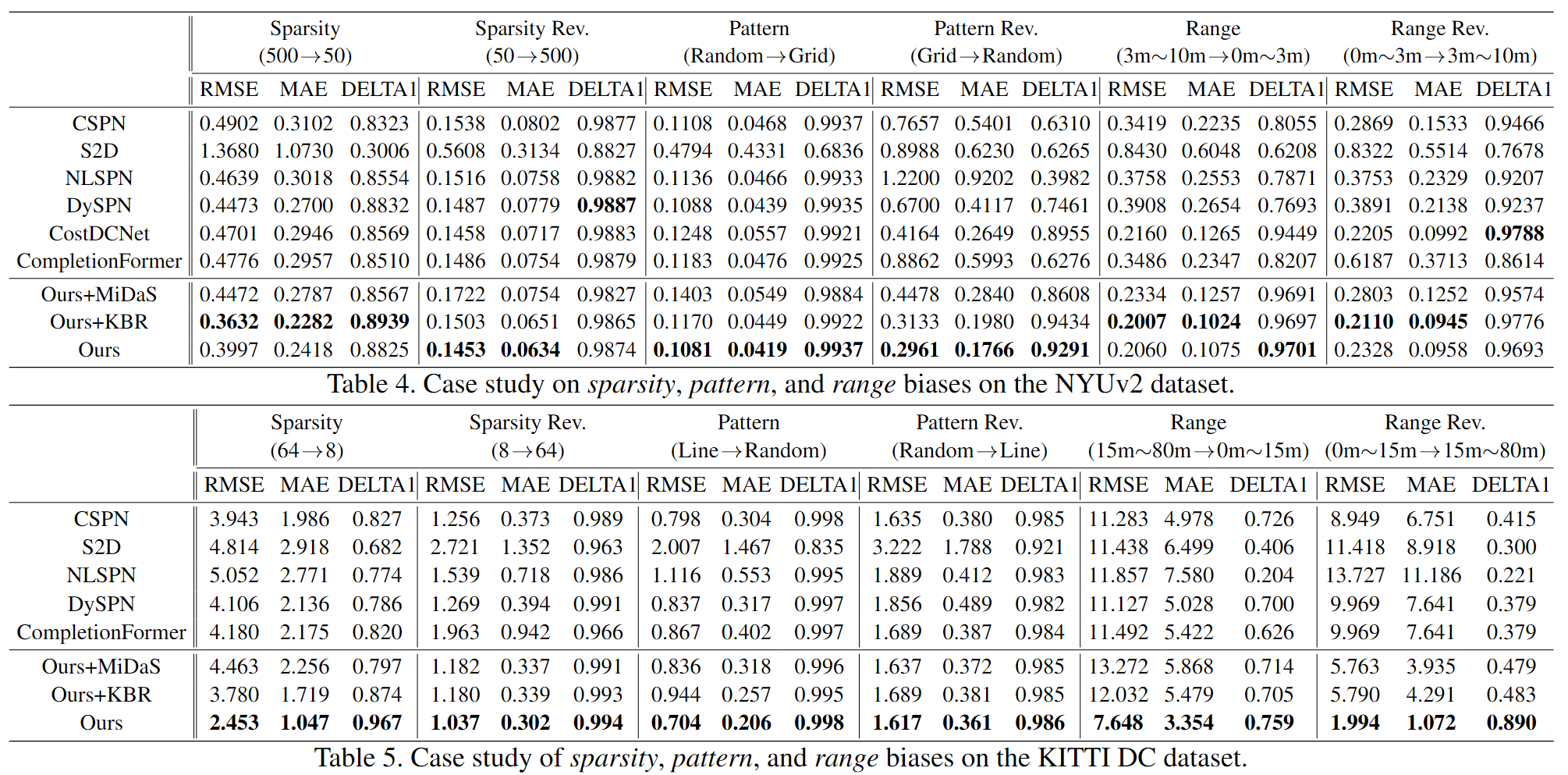
深度估计中的传感器偏差

depthprompting-1

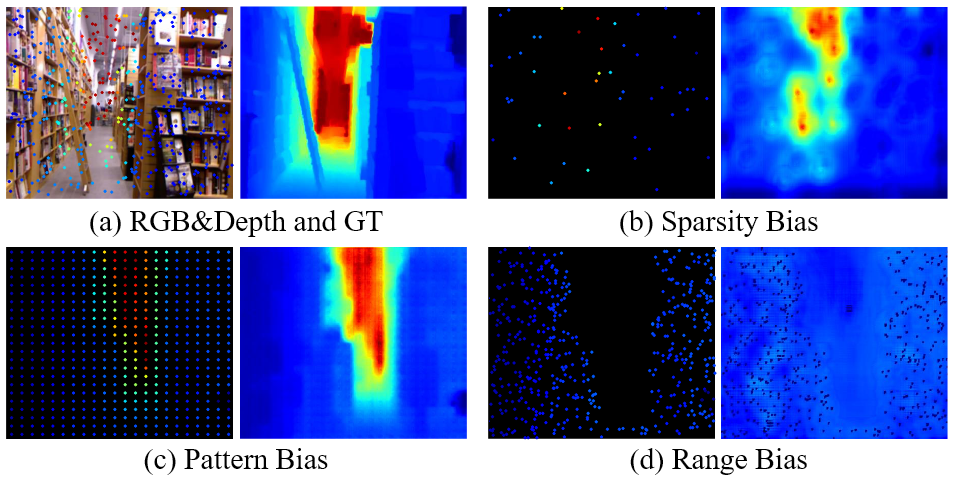
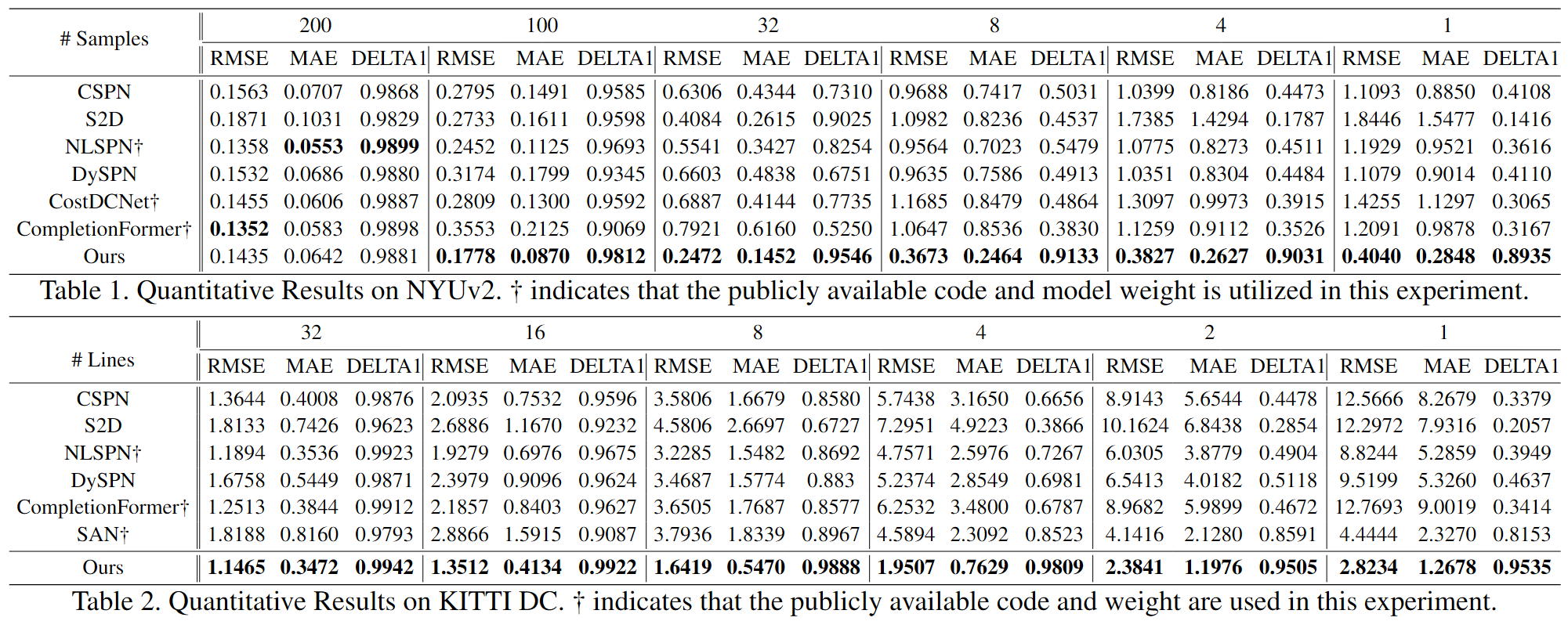
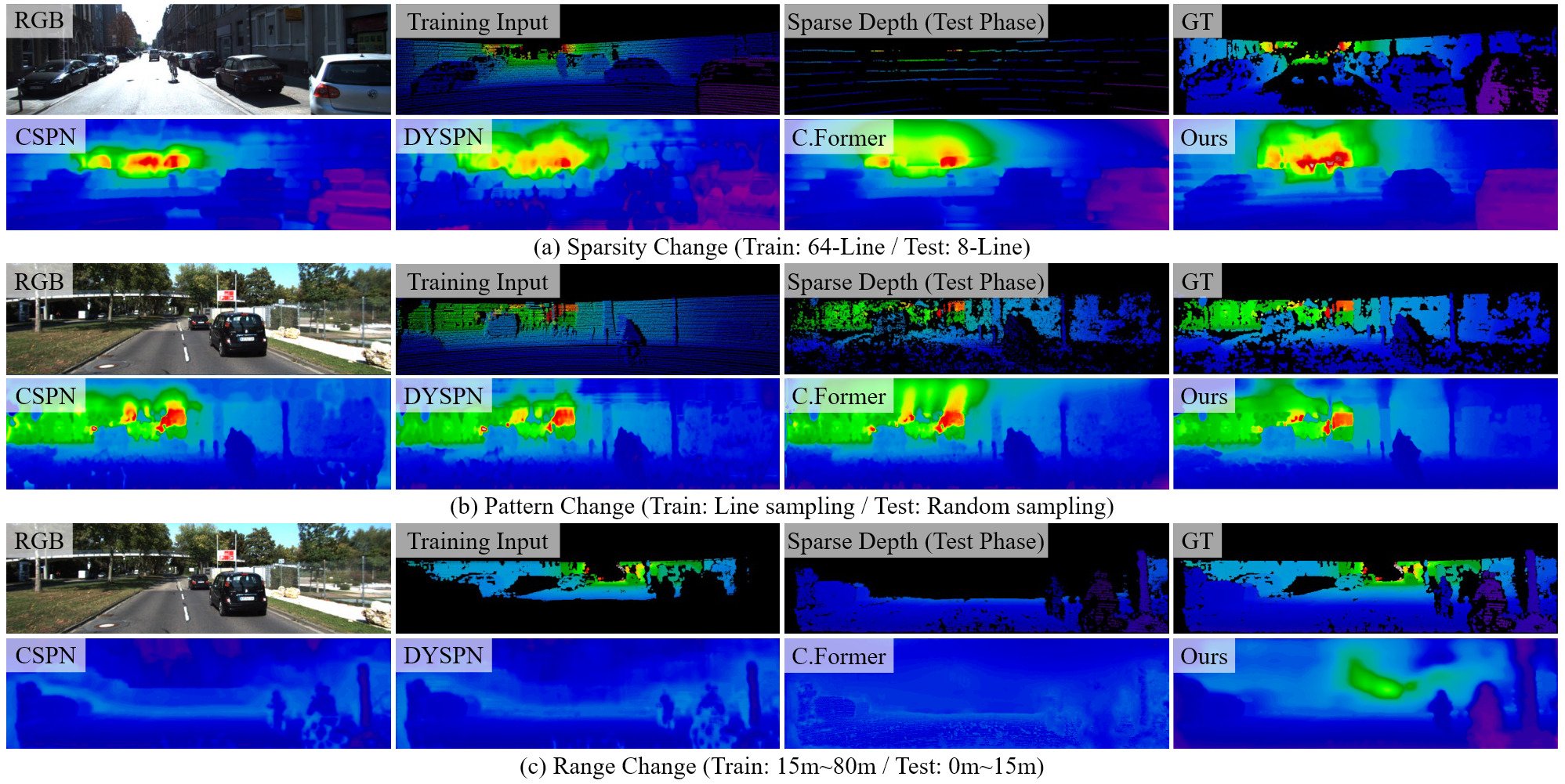
若一个基于学习的模型在特定密度（例如500个随机采样）上进行训练，就会收到稀疏性偏差的影响，如果在测试阶段只能见到更少的样本，就很难得到高保真的深度图。

其次，若训练和测试时的深度模式（样本的分布形式）不同，即使是相同的采样数量，也会导致模型性能的下降。在推理阶段改变输入的深度模式，会导致模型的预测偏向于输入的深度点。

最后，若场景结构在传感器有限的扫描范围之外时，会出现范围偏差。

深度提示

空间传播

将深度提示重新解释为空间传播，根据图像相关的亲和力权重，从输入的稀疏测量预测稠密的深度图，

传统的空间传播过程为

$\begin{align*} D^{t+1}_{(x,y)} = &\, A(x,y) \odot D^0_{(x,y)} + \sum_{(l,m) \in \mathcal{N}_{(x,y)}} A(l,m) \odot D^t_{(l,m)}, \quad \text{(1)} \end{align*}$

其中$D^{t}_{(x,y)} \in \mathbb{R}^{1 \times H \times W}$表示每一传播步骤$t$对应的深度图，$(x,y)$和$H$，$W$表示空间坐标和输入图像的高和宽。$D^0_(x,y)$ 和$A$表示初始的深度和逐像素的亲和力图。$\odot$操作表示逐元素相乘。$(l,m) \in \mathcal{N}_{(x,y)}$表示参考像素$(x,y)$的八方向的邻像素。

为了使亲和力图能够自适应不同的输入类型，设计了一个深度的编码器，来学习不同传感器的特征，并将它们投影到统一的嵌入空间。

深度特征提取

采用了编码器-解码器的结构来编码深度图的位置和空间信息。编码器将深度图作为输入，解码器重建出亲和力图。然后提示嵌入和图像特征融合获得边缘和语义信息。

具体的，使用ResNet34来提取深度特征，对特征进行2、4、8、16、32倍的下采样，然后通过跳连接输入解码器。给定稀疏的深度$D_S$，深度提示编码器$f_{\mathcal{E}}$产生提示嵌入$F_d$和多尺度的特征$F^{d}_k$

$F^d, F_k^d = f_{\mathcal{E}}(D_S), \tag{2}$

深度基础模型

给定单张图像$I \in \mathbb{R}^{3 \times H \times W}$，预训练深度模型$f_\mathcal{F}$输出初始的深度图$\hat{D}_I$和多尺度的中间特征$F^i_k$

$\hat{D}_{I}, F_{k}^{i} = f_{\mathcal{F}}(I, \Theta_{f_{\mathcal{F}}}), \tag{3}$

其中$\Theta_{f_{\mathcal{F}}}$ 表示基础模型的参数，在训练和推理过程中都冻结。

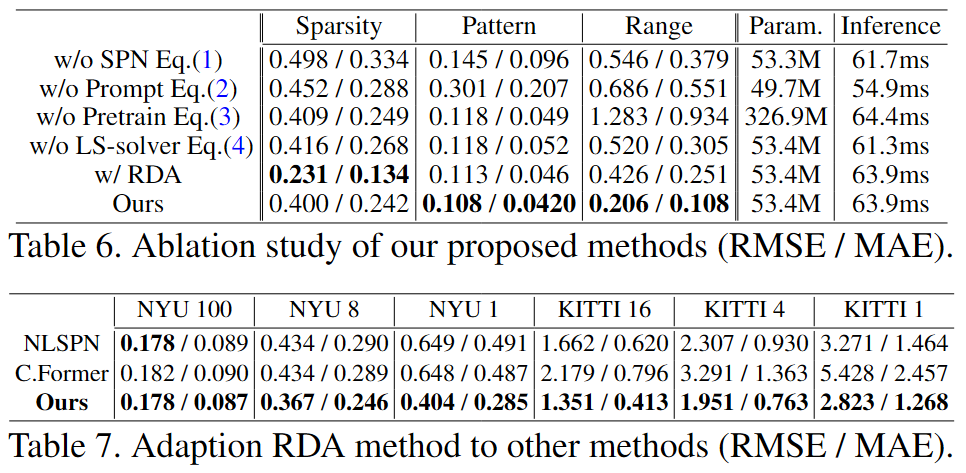
采用偏差微调技术，更新偏差项，冻结剩余的参数。为了推理得到绝对尺度的深度图，将基础模型获得的相对深度与传感器测量值进行融合。由于在空间传播的过程中，没有初始深度的地方不能够得到合理的深度值，所以采用了最小二乘求解器来获得一致的$D_I$。使用基础模型的初始深度和稀疏的深度$D_S$进行全局的优化。对应的最小二乘的解为：

$\hat{p} = \min_{p} \| p \hat{D}_I^V - D_S \|_F, \tag{4}$

其中$| \cdot |_F$表示Frobenius范数，$ D^{V} _{I}\subset \hat{D}_{I}$表示一组对应合理深度点的像素。最小二乘的解$\hat{p}$和初始深度$\hat{D}_I$相乘得到公式1中的$D^0_{(x,y)}$

用于自适应亲和力图的解码器

利用基础模型编码器得到的图像嵌入和提示编码器得到的提示嵌入来重建亲和力图。将提示嵌入$F_d$，中间特征$F^{d}_i$和多尺度图像特征$F^{i}_k$连接，然后得到$A_{\text{ada}} \in \mathbb{R}^{C^2 \times H \times W}$。其中$C$是超参数，定义传播的范围，设置为7

$A_{\mathrm{ada}} = f_D (F^d, F^d_k, F^i_k). \tag{5}$

实施细节

随机深度增强。从相对稠密的深度图中采样深度点来模拟稀疏的输入深度。此外还在通用和极端条件下进行训练（从500个随机样本到只有1个深度点）。

损失函数

对深度基础模型的初始深度应用尺度不变损失，联合使用$L_1$、$L_2$损失得到最终的稠密深度。

尺度不变损失

$L_{\mathrm{SI}}(\hat{D}_{I}, D^{gt}) = \frac{1}{|V|} \sum_{v \in V} (\delta_{v})^{2} - \frac{\lambda}{|V|^{2}} \left( \sum_{v \in V} \delta_{v} \right)^{2}, \tag{6}$

联合损失

$L_{\text{comb}}(\hat{D}, D^{gt}) = \frac{1}{|V|} \sum_{v \in V} \left( \left| \hat{D}(v) - D^{gt}(v) \right| + \left| \hat{D}(v) - D^{gt}(v) \right|^2 \right), \tag{7}$

最终总的损失

$\mathcal{L} = L_{\mathrm{comb}}(\hat{D}, D^{gt}) + \mu L_{\mathrm{SI}}(\hat{D}_I, D^{gt}) \tag{8}$

$\mu$设置为0.1

depthprompting-2