摘要

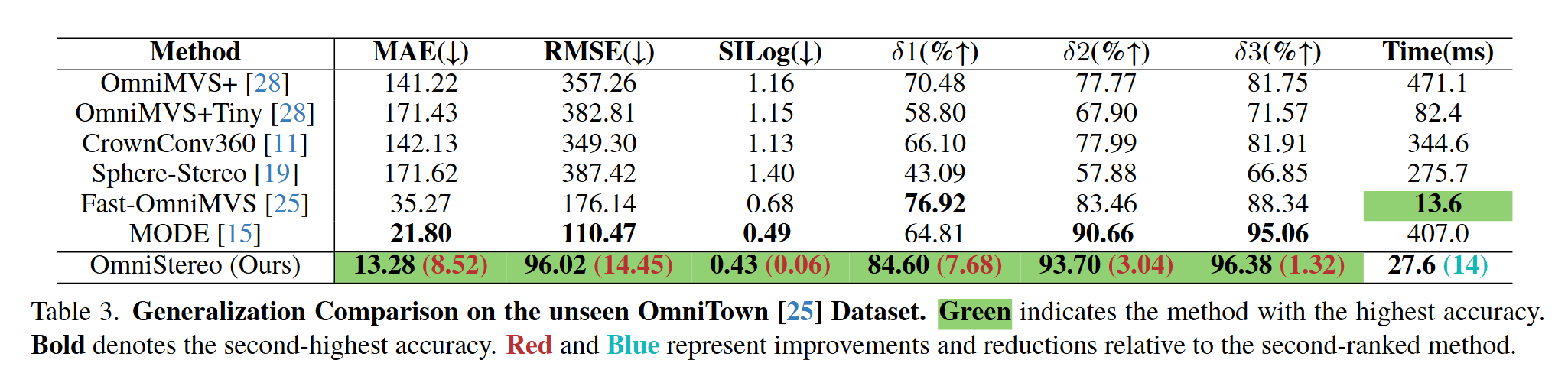
快速可信的全向三维感知对许多应用都十分重要。虽然许多公认的方法能够产生高质量的全方位三维信息，但是对于实时计算太慢了。

提出了一种高效的全方位深度感知框架OmniStereo。使用卡西尼投影来简化光度匹配。提出了一个轻量化的立体匹配网络来最小化计算开销。提出了一种新的融合方法来处理深度不连续和无效像素，辅以细化模块来减少映射引入的误差并恢复精细细节。

简介

传统使用激光雷达和多个立体相机来获取全向三维信息，但激光雷达往往十分昂贵且笨重，只能产生稀疏的三维扫描，缺少视觉表面信息。立体相机的不同相机之间也存在盲点。因此使用少量的鱼眼相机能够减少系统重量与成本。

鱼眼相机复杂的几何约束和图像失真对全方位深度估计提出了挑战。一方面，目前的方法仍然存在精度问题，如分层不均匀和映射引入的误差。同时，模型对未知场景的可迁移性远不能令人满意。

另一方面，采用深度神经网络计算复杂度高，当前方法在处理多张鱼眼图像时存在严重的延迟。这些方法通常构建包含冗余信息的广泛4D代价体，或者需要学习复杂的极线几何。近期的方法也在实时性能方面也取得了长足进步，但是在复杂场景下深度估计精度较差，忽略了视图间的深度不连续性，无法处理多视角深度融合时的不合理的像素。

方法

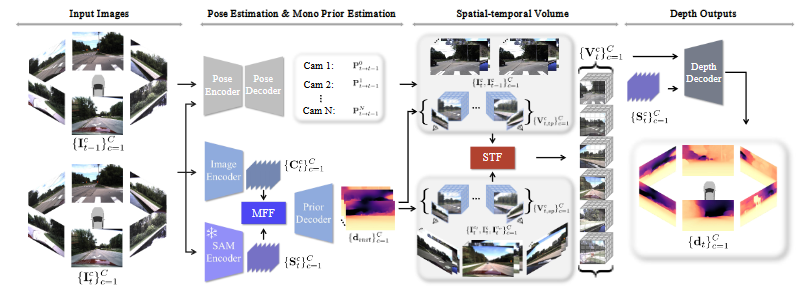
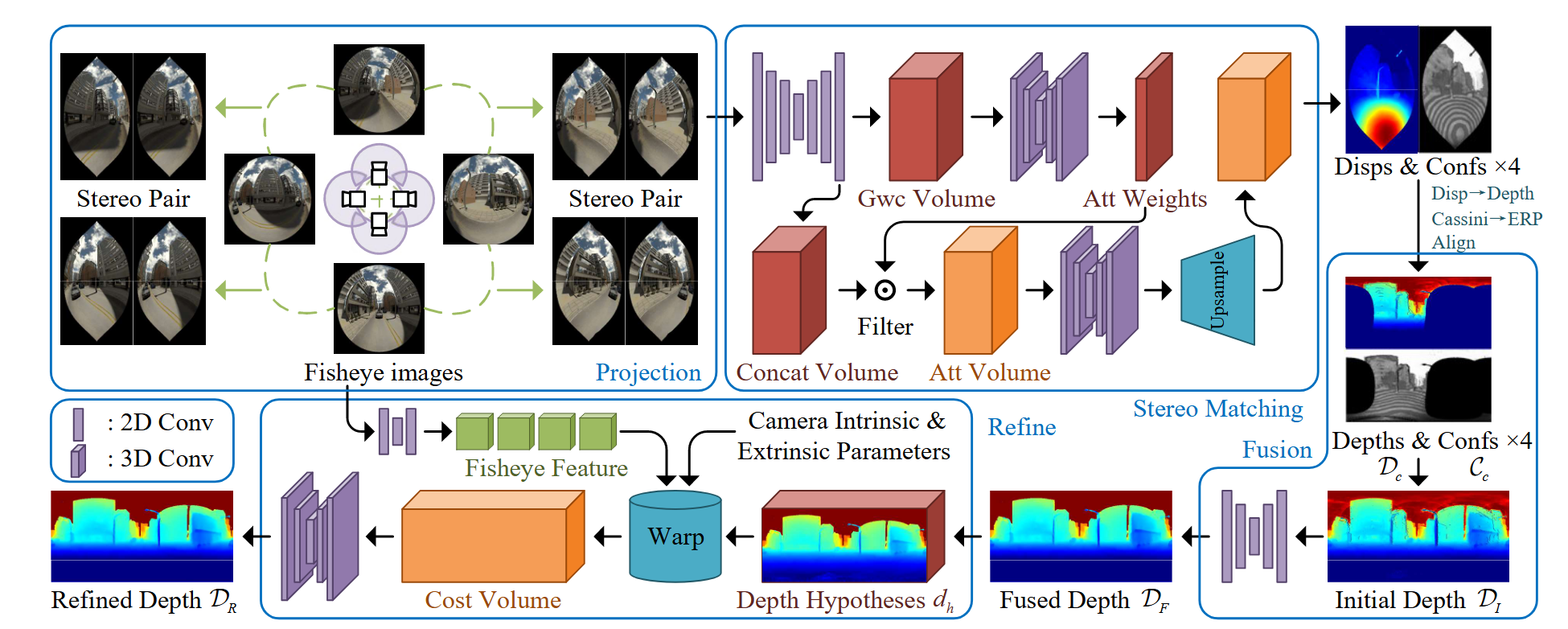
包含四个部分：投影，立体匹配，多视角融合与深度细化

OmniStereo-0

卡西尼球坐标系

相较于针孔投影活立方体投影，卡西尼投影能够用更少的投影操作提供更广的视场角。

首先用鱼眼相机模型将鱼眼图像投影到空间笛卡尔坐标系中的单位球上，然后转换到卡西尼球坐标系，最终投影为卡西尼投影图像。

OmniStereo-1

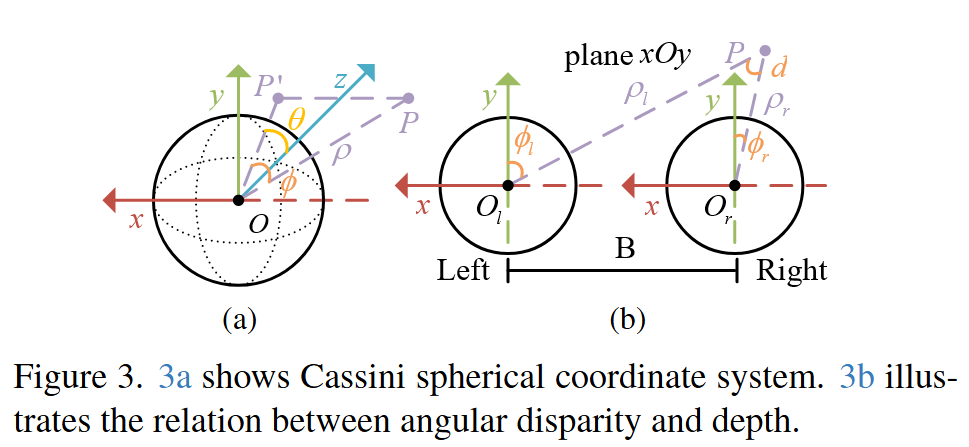
卡西尼球坐标系定义为$(\rho,\phi,\theta)$，其中$\rho$表示原点$O$与点$P$之间的距离；$\phi$是$OP$和$yOz$平面之间的夹角；$\theta$是$OP’$和正$z$轴之间的夹角，$P’$表示点$P$到$yOz$平面的投影点，笛卡尔坐标系到卡西尼球坐标系的转换如下：

$\begin{cases} x=\rho s i n \left( \phi\right) \\ y=\rho c o s \left( \phi\right) s i n \left( \theta\right) \\ z=\rho c o s \left( \phi\right) c o s \left( \theta\right) \\ \end{cases} \quad\begin{cases} \rho=\sqrt{x^{2}+y^{2}+z^{2}} \\ \phi=a r c s i n \left( \frac{x} {\rho} \right) \\ \theta=a r c t a n \left( \frac{y} {z} \right) \\ \end{cases}\tag{1}$

在卡西尼投影域中，视差$d$表示为水平角$\phi$之间的差距，定义为$d=\phi_l-\phi_r$。从点$P$到原点$O$的深度$\rho_1$可以用下式计算，其中$B$表示基线长度

$\rho_{l}=B \cdot\frac{s i n \left( \phi_{l}-d+\frac{\pi} {2} \right)} {s i n \left( d \right)} \tag{2}$

轻量深度估计

在卡西尼投影域中，极线会投影为水平线，能够简化光度匹配。在这里OmniStereo将立体匹配的模块是为高效的深度初始化器，快速生成粗糙的深度估计$\mathcal{D}_c$。

从ACVNet中获得灵感，从Gwc volume生成的注意力权重中过滤concatenation volume，构建低分辨率、紧凑、冗余最小的attention volume。应用CUBG对代价体进行上采样，生成可信的视差图与置信度图$\mathcal{C}_c$。最后使用公式2将视差转换为深度$\mathcal{D}_c$。

置信度引导的融合模块

在立体匹配中，在不同的方向都生成了深度$\mathcal{D}_c$，为了构建全方位深度图，需要将这些深度图转换到ERP域。但是直接用相机外参将他们拼接在一起会引入深度不连续与不合理的像素。第一步，估计初始的深度$\mathcal{D}_I$来消除深度不连续性。第二步，使用一个网络来填充不合理的像素。

立体匹配首先根据概率体，对深度假设取加权和来估计视差。如果估计的视差接近真实值，估计值的概率也会近似于真实概率。

第一步，深度图$\mathcal{D}_c$和置信度图$\mathcal{C}_c$转换为ERP域的统一视角，得到置信度图$\mathcal{C}_u$和深度图$\mathcal{D}_u$。对于视场角以外的区域，置信度设置为-∞。初始的全方位深度图$\mathcal{D}_I$由下式计算：

$\mathcal{D}_{I}=\sum_{i=1}^{M} \mathcal{D}_{u, i} \cdot\sigma\left( \mathcal{C}_{u, i} \right) \tag{3}$

其中$M$是立体对的数量，$\mathcal{D}_{u,i}$和$\mathcal{C}_{u,i}$表示第$i$个立体对的深度图和置信度图。$\sigma$白哦是softmax操作。

由于遮挡和视角变换，初始的全方位深度图包含不合理的像素。在第二阶段，采用网络使用相邻像素的深度信息来产生融合的深度图$\mathcal{D}_F$。网络结构为编码器-解码器结构。

全方位深度优化

为了细化融合的深度$\mathcal{D}_F$，在小的邻域内的每个像素深度周围进行有限的均匀采样来生成深度假设$d_h$。使用鱼眼相机成像模型和深度假设，输入图像的特征图被warp到不失真的球表面上：

$P_{k} \left( \theta, \phi\right)=\Pi\left( T_{i}, \left( d_{h, k} \cdot P_{u} \left( \theta, \phi\right) \right) \right) \tag{4}$

其中

$P_{u} \left( \theta, \phi\right)=\left( c o s \left( \phi\right) c o s \left( \theta\right), s i n \left( \theta\right), c o s \left( \phi\right) s i n \left( \theta\right) \right)^{\top}$

表示单位球上的三维点。$\prod$表示将三维点投影到鱼眼图像的投影模型。$T_i$表示第$i$个相机的内外参，$d_{h,k}$表示第$k$个深度假设。

使用公式4，特征图被warp来构建一个小的四维代价体。一个轻量的沙漏网络用来进行代价聚合。最终的优化深度$\mathcal{D}_R$用softargmin函数获得：

$\mathcal{D}_{R}=\sum_{i=1}^{N} d_{h, k} \cdot\sigma\left( C_{i} \right) \tag{5}$

其中$C$是代价体，$N$是深度假设的数量。