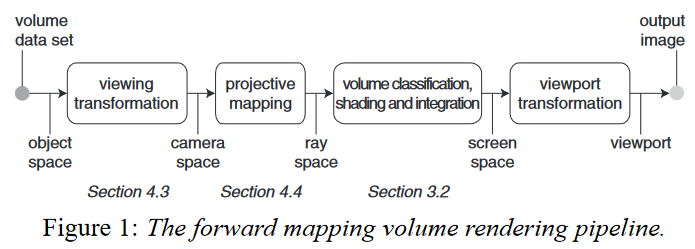
EWA Volume Splatting
elliptical Gaussian kernels 椭圆高斯核 Splatting algorithms interpret volume data as a set of particles that are absorbing and emitting light. 泼溅算法将体素数据解释为一组吸收和发射光的粒子。 Our method is based on a novel framework to compute the footprint function, which relies on the transformation of the volume data to so-called ray space. This transformation is equivalent to perspective projection. By using its local affine approximation at each voxel, we derive an analytic expression for the EWA footprint in...
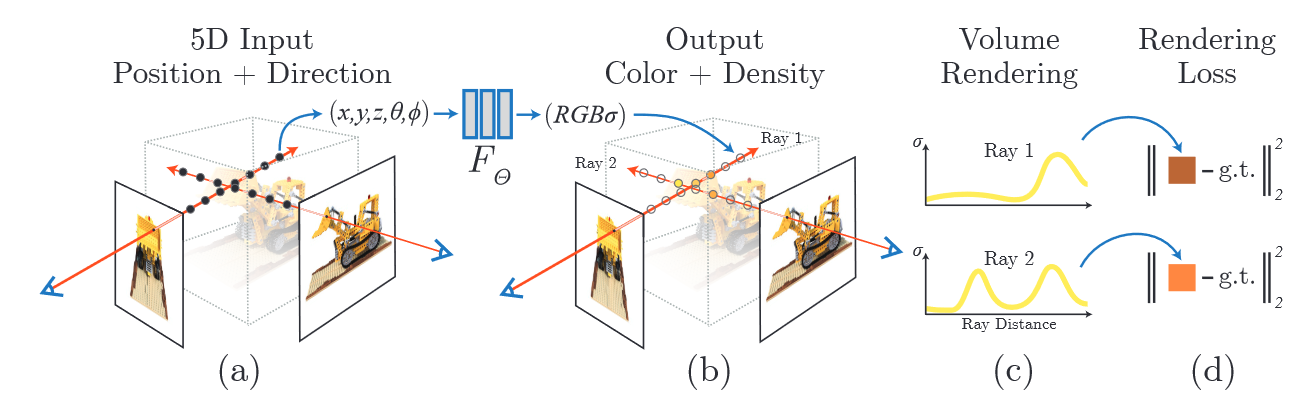
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
Neural Radiance Field Scene Representation输入:连续的5D坐标(空间位置+视角方向) 3 \mathrm{D ~ l o c a t i o n ~} \mathbf{x}=( x, y, z ) \mathrm{2 D ~ v i e w i n g ~ d i r e c t i o n ~} ( \theta, \phi)输出:空间位置上的体密度和辐射强度 \mathrm{emitted color}~{\bf c}=( r, g, b ) \mathrm{v o l u m e \ d e n s i t y} \ \sigma密度控制了穿过某一位置的光线在那个位置累积了多少辐射 方法简单总结: 1)将相机光轴穿过场景生成采样的三维点集 2)用三维点和对应的二维视角方向输入神经网络生成颜色和密度集 F_{\Theta} : ( {\bf x}, {\bf d} ) \to( {\bf c},...
Mip-Splatting: Alias-free 3D Gaussian Splatting
3DGS在改变采样率或者改变焦距和相机距离时,会存在严重的膨胀效应和高频伪影 采样理论(奈奎斯特-香农采样理论)对连续信号的采样频率至少是最大频率的两倍,所以在采样之前要对信号施加滤波。 3DGS中的Dilation操作为了防止投影的2DGS小于一个像素,所以投影的2DGS进行了膨胀操作: {\mathcal G}_{k}^{2 D} ( \mathbf x )=e^{-{\frac{1} {2}} ( \mathbf x-\mathbf p_{k} )^{T}} ( \mathbf\Sigma_{k}^{2 D}+s \, \mathbf I )^{-1} \, ( \mathbf x-\mathbf p_{k} ) \tag{5}Sensitivity to Sampling Rate 对于Zoom-out,原本的object在像素中的占比缩小了,所以为了要膨胀到一个像素的大小,施加的二维膨胀相较于原来更大 对于Zoom-out,原本的object在像素中的占比变大,所以膨胀到一个像素大小所需的二维膨胀就更小 it leads to erosion effects...
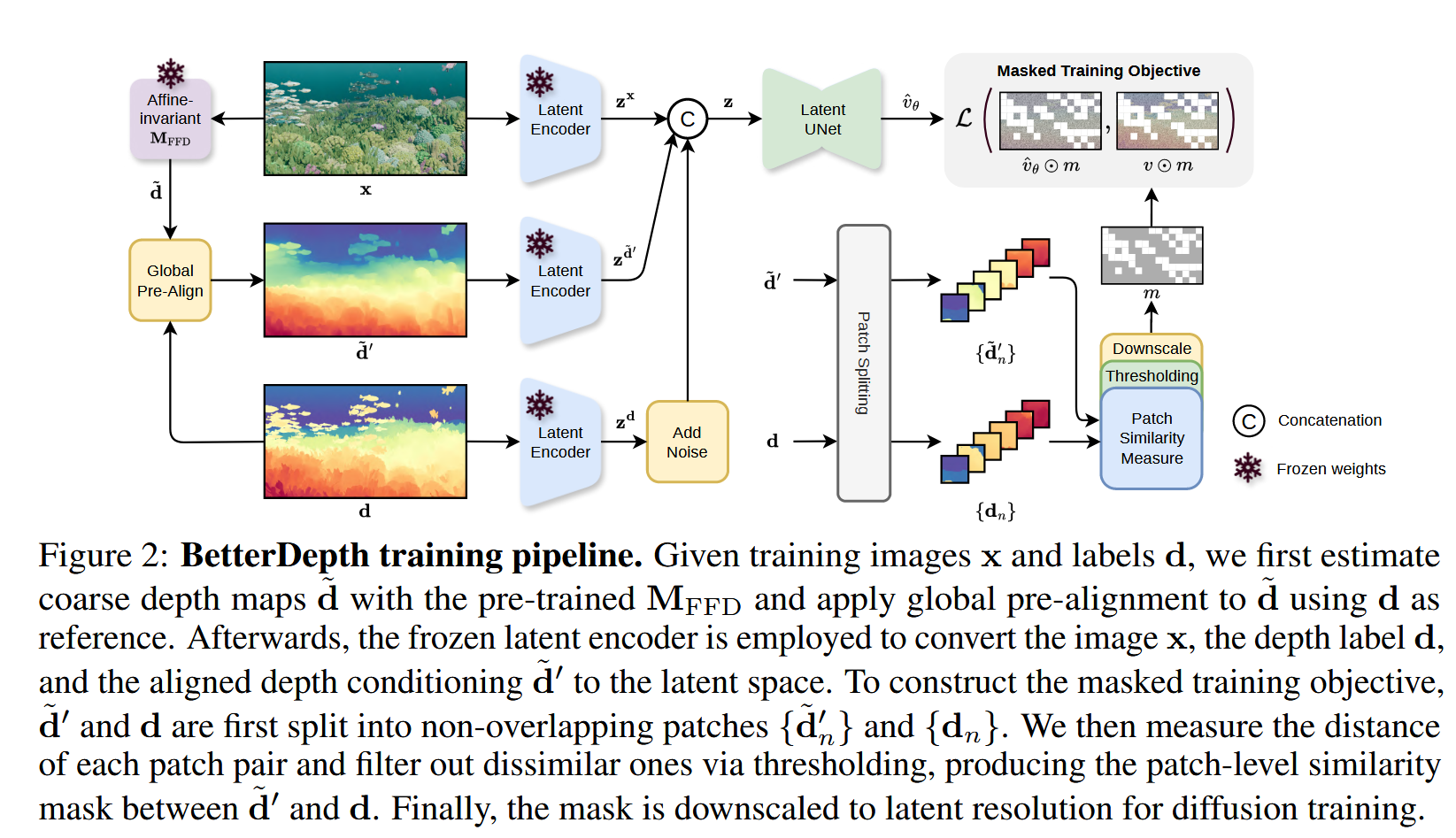
BetterDepth: Plug-and-Play Diffusion Refiner for Zero-Shot Monocular Depth Estimation
Problem Formulationfeed-forward model: {\cal L}_{\mathrm{M D E}} ( {\bf d}_{i}, {\bf M}_{\mathrm{F F D}} ( {\bf x}_{i} ) ), \tag{1}Diffusion model: {\cal L}_{\mathrm{D M}} \left( \epsilon, {\bf M}_{\mathrm{D M}} \left( {\bf x}_{i}, \mathrm{A d d N o i s e} ( {\bf d}_{i}, \epsilon, t ) \right) \right), \tag{2}Framework Global Pre-Alignment给定预训练仿射不变深度模型$\bf{M}_{FFD}$ 和数据对$\bf{(x, d)} ∈ \bf{D}_{syn}$...
DIFFERENTIABLE 3D GAUSSIAN SPLATTING
3D高斯的优势:非结构化、可微、利用快速α混合进行渲染、无需法线 世界坐标系下,高斯由三维协方差矩阵和点(均值)μ表示: G ( x ) \,=e^{-\frac{1} {2} ( x )^{T} \Sigma^{-1} ( x )} \tag{4}给定视角变换矩阵W,相机坐标系下的协方差矩阵为: \Sigma^{\prime}=J W \Sigma W^{T} J^{T} \tag{5}其中J是投影变换的仿射近似雅可比矩阵 协方差矩阵只有在半正定的时候才具有物理意义,而如果直接对协方差矩阵使用梯度下降优化,很难保证矩阵的合理性。 由于协方差矩阵是用来描述椭球的形状,因此可以用缩放矩阵S和旋转矩阵R来获得一个对应的协方差矩阵: \Sigma=R S S^{T} R^{T}\tag{6}OPTIMIZATION WITH ADAPTIVE DENSITY CONTROL OF 3D GAUSSIANSOptimization优化的参数:位置p,α,协方差矩阵,球谐函数系数 \mathcal{L}=( 1-\lambda)...
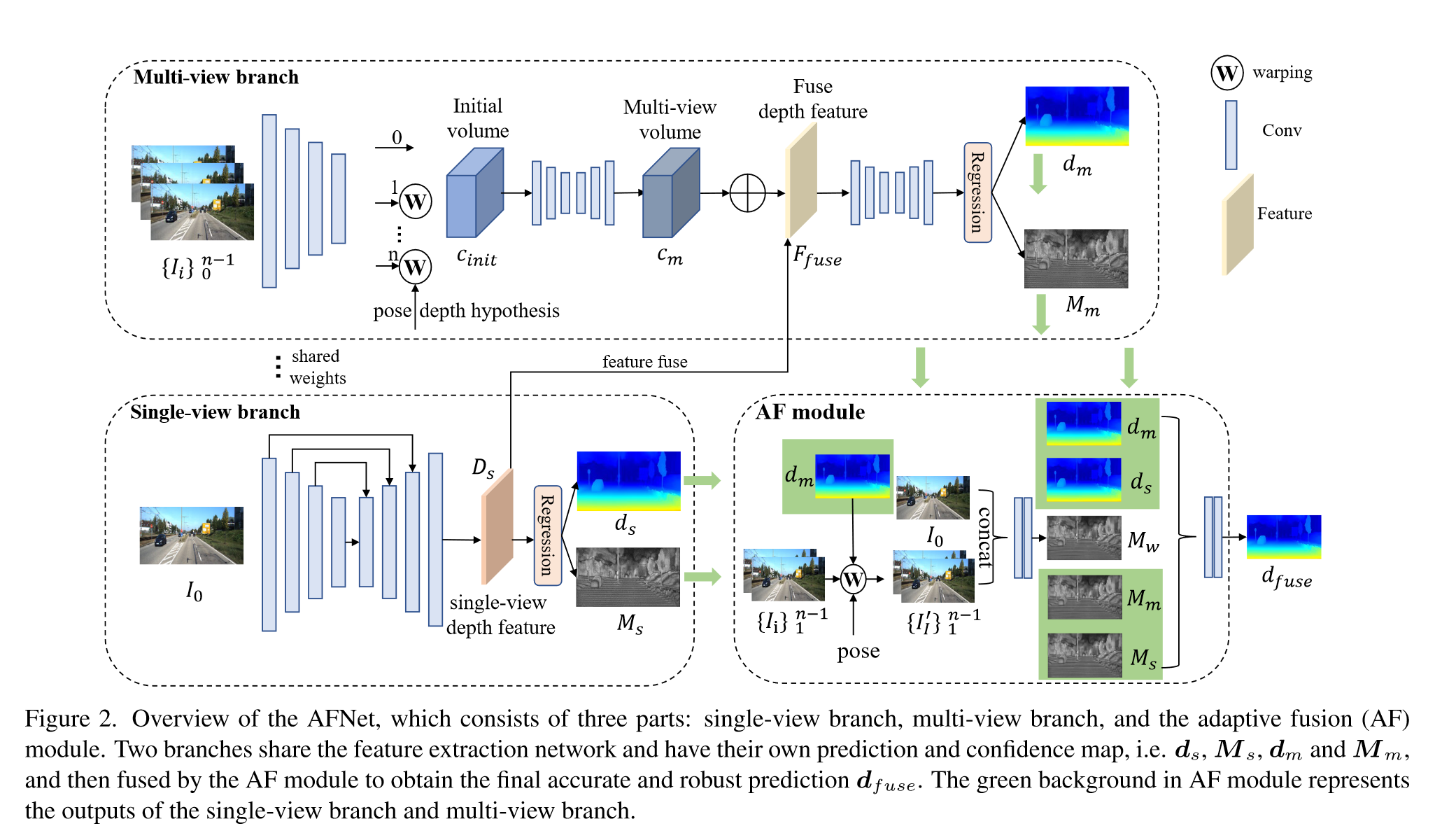
Adaptive Fusion of Single-View and Multi-View Depth for Autonomous Driving
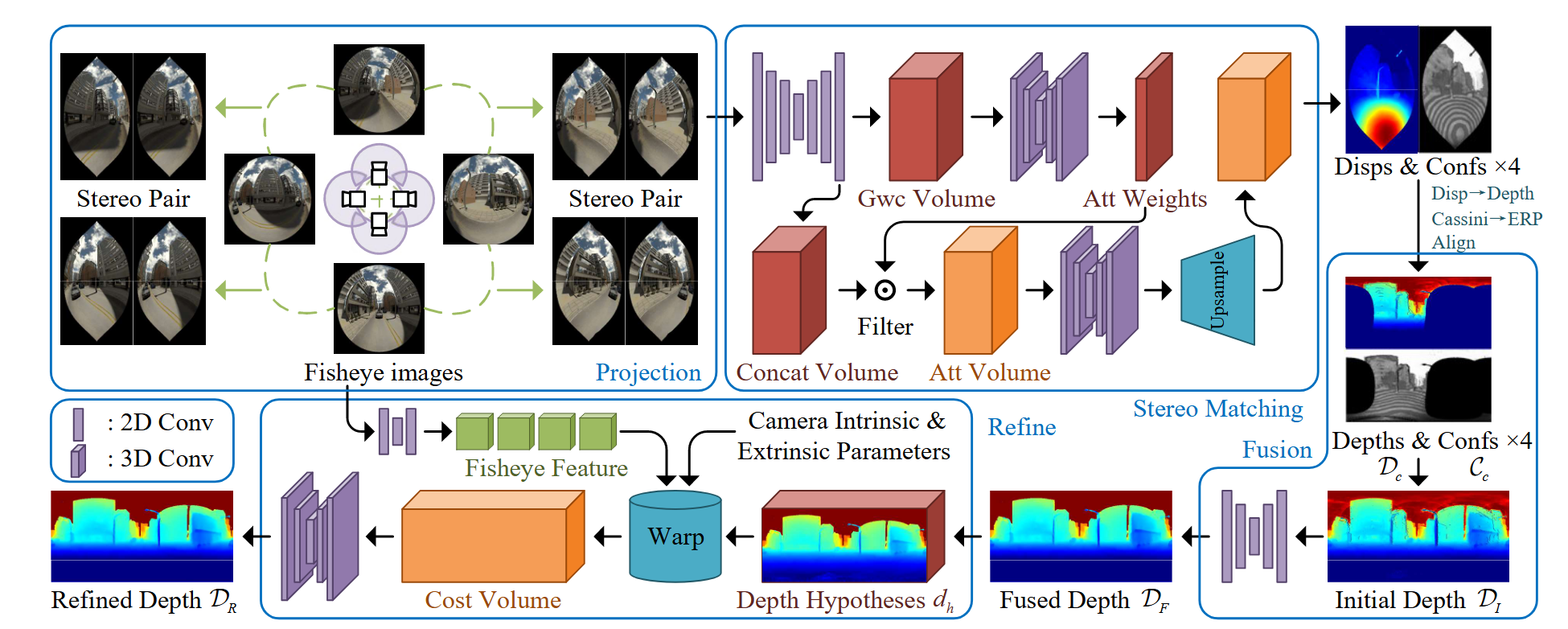
Input: $n-1$ 个源图像 ${I_i}^{n-1}_{i=1}$、参考图像 $I_0$、相机内参和相机姿态 Output:depth $d$ Part:single-view depth module, multi-v iew depth module, adaptive fusion module and pose correction module Single-view and Multi-view Depth Module使用ConvNeXt-T作为backbone提取四个尺度上的特,征$F_{ i,l} (l = 1, 2, 3, 4)$,特征维度分别为$C=96,192,384,768$ Single-view branch采用多尺度的decoder聚合特征获得深度特征$D_s ∈ R^{H/4×W/4×257}$ 对$D_s$的前256个通道使用softmax得到depth probability volume $P_s ∈ R^{H/4×W/4×256}$,最后一个通道作为置信度图$M_s ∈...
SSD:Stealing Stable Diffusion Prior for Robust Monocular Depth Estimation
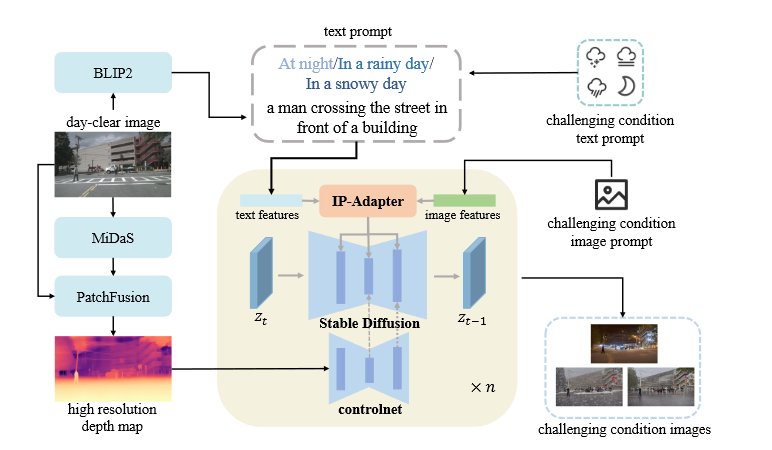
背景现有的MDE方法在标准的环境下(例如晴天)表现的很好,但是在一些具有挑战性的条件下效果会变得很差,这主要是由于一些关键的假设失效了,例如光度一致性假设,同时也没有可靠的ground truth包含这些场景。 现有的一些鲁棒的解决方案 基于模型的方法 这一方法通过修改网络结构来增强模型处理各种条件的能力 缺点:网络模型过于复杂,不能够适应各种环境 基于数据的方法 利用域自适应或其他模态的数据来增强图像信号 缺点:缺乏高质量的数据,需要后处理 方法Generative Diffusion Model-based Translation生成在深度方面与白天清晰图像非常相似的训练样本 I_{g}=S D ( I P ( T_{p}, I_{p} ), C N ( D_{h} ), z ) BILP2:获取场景描述符,保留图像内容信息 ControlNet d2i:保持近似深度一致性 MiDas:获取初始深度图 PatchFusion:获得高分辨率的深度图 text prompt=BILP2 场景描述符+challenging condition...
md4all:Robust Monocular Depth Estimation under Challenging Conditions
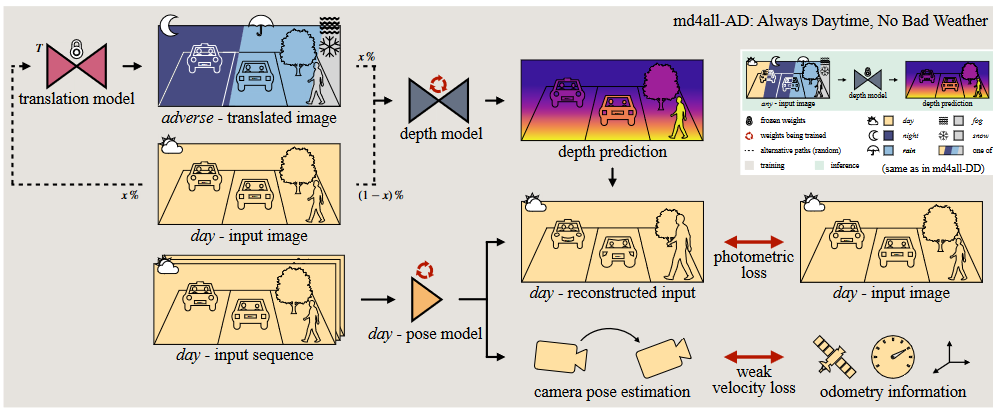
md4all-AD: Always Daytime, No Bad Weather输入图像经过depth model得到prediction,然后将源图像warp到目标视角中,利用monodepth2中的最小重投影误差L_p进行监督,忽略静态像素。 {\mathcal{L}}_{1} ( I_{t}, {\hat{I}}_{t} )=\left\| I_{t}-{\hat{I}}_{t} \right\|_{1} {\cal L}_{\mathrm{S S I M}}=1-\mathrm{S S I M} \left( I_{t}, \hat{I}_{t} \right) p e \left( I_{t}, \hat{I}_{t} \right)=\left( 1-\alpha\right) {\mathcal{L}}_{1} ( I_{t}, \hat{I}_{t} )+{\frac{\alpha} {2}} {\mathcal{L}}_{\mathrm{S S I M}} ( I_{t}, \hat{I}_{t} ) \mathcal{L}_{p} \left(...
pixelSplat: 3D Gaussian Splats from Image Pairs for Scalable Generalizable 3D ReconstructionpixelSplat
3D GS中的局部最小值问题在随机位置初始化的高斯,在移向最终位置的时候会出现局部最小值: 1.如果距正确位置的距离超出一定的标准差范围后,高斯元的梯度会消失 2.即使高斯足够接近一个“正确”的位置,仍然需要一个通向最终位置的路径,使得损失在路径上单调减少。 3D高斯虽然通过自适应的密度控制来让高斯移到最终的位置,但是这种方法与一般的设定不相容,一般来说参数都需要通过一个神经网络来预测,必须接收梯度。 以图像为条件的3DGS推理解决尺度模糊问题在理想情况下,新视角合成的数据集包含的相机位姿应当是metric的,每一个场景应当包含一系列元组 {\mathcal{C}}_{i}^{\mathrm{m}} =\{( \mathbf{I}_{j}, \mathbf{T}_{j}^{\mathrm{m}} ) \}_{j}包括图像和对应的真实世界尺度的位姿。 在实际的情况下,数据集中的位姿通常是使用SfM计算的,每一个场景都对应着不同的尺度,这时 s_{i} \mathbf{T}_{j}^{\mathrm{m}}对应的才是metric的位姿。 给定两个参考视角...
NVDS+: Towards Efficient and Versatile Neural Stabilizer for Video Depth Estimation
整体网络结构与NVDS保持一致 稳定网络深度感知特征编码对于一个滑动窗口中的一组初始深度图 $F^{norm}_i={F_1,F_2,F_3,F_4}$ ,其归一化的方式为: F_{i}^{n o r m}=\frac{F_{i}-\operatorname* {m i n} \left( \mathbf{F} \right)} {\operatorname* {m a x} \left( \mathbf{F} \right)-\operatorname* {m i n} \left( \mathbf{F} \right)} \,, i \in\left\{1, 2, 3, 4 \right\}. \tag{1}将归一化后的深度图与RGB图像连接形成RGBD序列,通过transformer backbone编码成深度感知的特征图 交叉注意力模块目标帧的特征图中的像素作为query,keys和values是从参考帧中生成的。 采用了patch merging的方法,并将交叉注意力机制限制在局部窗口内,减小计算开销。 用 $T$...